- 二项式定理的应用
- 共36题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额。
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求:
①顾客所获的奖励额为60元的概率;
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和50元的两种球组成,或标有面值20元和40元的两种球组成,为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由。
正确答案
(1)设顾客所获取的奖励额为X,
①依题意,得P(X=60)=
即顾客所获得奖励额为60元的概率为
②依题意得X得所有可能取值为20,60,
P(X=60)=

即X的分布列为
X 60 20
P 
所以这位顾客所获的奖励额的数学期望为E(X)=20×

(2)根据商场的预算,每个顾客的平均奖励额为60元,所以先寻找期望为60元的可能方案。
对于面值由10元和50元组成的情况,如果选择(10,10,10,50)的方案,因为60元是面值之和的最大值,所以数学期望不可能为60元,
如果选择(50,50,50,10)的方案,因为60元是面值之和的最小值,所以数学期望也不可能为60元,
因此可能的方案是(10,10,50,50)记为方案1,
对于面值由20元和40元的组成的情况,同理可排除(20,20,20,40)和(40,40,40,20)的方案,所以可能的方案是(20,20,40,40),记为方案2,
以下是对这两个方案的分析:
对于方案1,即方案(10,10,50,50)设顾客所获取的奖励额为X1,则X1的分布列为
X1 60 20 100
P 

X1 的数学期望为E(X1)=
X1 的方差D(X1)=

对于方案2,即方案(20,20,40,40)设顾客所获取的奖励额为X2,则X2的分布列为
X2 40 20 80
P 

X2 的数学期望为E(X2)=
X2 的方差D(X2)=差D(X1)

由于两种方案的奖励额的数学期望都符合要求,但方案2奖励额的方差比方案1小,所以应该选择方案2。
解析
概率与统计。
(1)根据古典概型的概率计算公式计算顾客所获的奖励额为60元的概率,依题意得X得所有可能取值为20,60,分别求出P(X=60),P(X=20),画出顾客所获的奖励额的分布列求出数学期望;
(2)先讨论,寻找期望为60元的方案,找到(10,10,50,50),(20,20,40,40)两种方案,分别求出数学期望和方差,然后做比较,问题得以解决。
知识点
观察下列各式:

正确答案
解析
知识点
如图5,









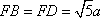

(1)证明:
(2)已知点


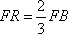

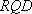
正确答案
见解析。
解析
(1)证明: 连结



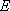
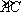
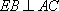
在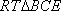

在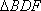



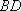
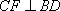
在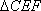

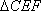
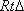
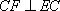
因为

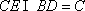

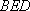
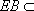


因为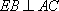
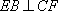


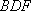
而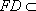


(2)设平面

由
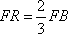

而
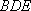
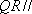
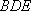
而平面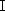


∴
由(1)知,
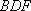


而
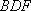
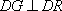

∴

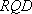
在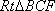

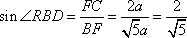

在

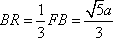
由余弦定理得,
由正弦定理得,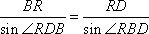
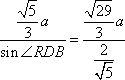

故平面

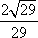
知识点
使
正确答案
解析





故最小的n值为5,故选B
知识点
扫码查看完整答案与解析