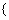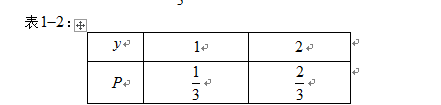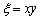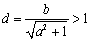- 二项式定理的应用
- 共36题
给出下列命题:
(1)已知事件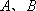
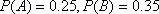
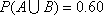
(2)已知事件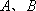
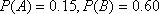
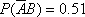
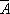
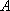
(3)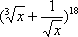
则其中真命题的序号是 [答]( )。
正确答案
解析
略
知识点
现有一枚质地均匀的骰子,连续掷两次,所掷的点数依次记为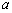
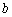
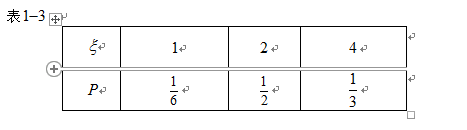
(1)若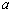
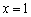
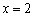
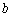
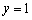
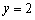
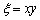
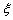
(2)设命题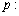
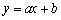
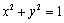
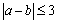
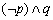
正确答案
见解析。
解析
(1)易知事件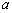
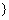
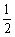
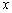
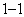
事件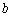
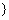
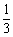
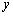
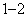
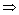
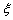
由上述二表可知: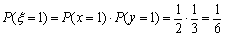
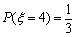
于是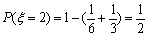
从而可知随机变量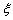
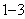
进而可知随机变量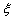
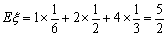
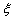
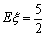
(2)命题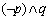
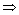
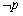
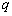
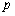
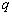
若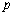
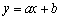
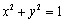
于是直线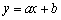
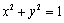
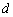
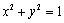
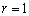
即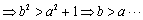
若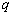
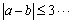
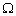
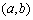
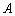
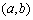
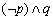
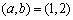
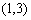
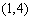
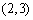
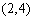

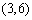
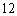
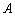
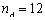
又易知事件

则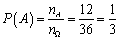
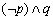
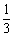
知识点
在

正确答案
1-
解析
略
知识点
在


正确答案
256
解析
略
知识点
已知


正确答案
6
解析
略
知识点
甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了频数分布统计表如下:
(1)计算x,y的值。
(2)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率;
(3)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异。
正确答案
见解析。
解析
(1)甲校抽取

故x=6,y=7,……………4分
(2)估计甲校优秀率为≈18.2%,乙校优秀率为=40%, …6分
(3)k2=
又因为6.109>5.024, 1-0.025=0.975,
故有97.5%的把握认为两个学校的数学成绩有差异。 …………12分
知识点
已知二项式






正确答案
2
解析
略
知识点
若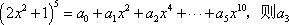
正确答案
80
解析
略
知识点
若

正确答案
解析
略
知识点
若
正确答案
解析
略
知识点
扫码查看完整答案与解析