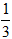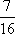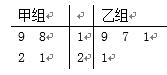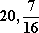- 随机事件的关系
- 共288题
有一个不透明的袋子,装有3个完全相同的小球,球上分别编有数字l,2,3。
(1)若逐个不放回取球两次,求第一次取到球的编号为偶数且两个球的编号之和能被3整除的概率;
(2)若先从袋中随机取一个球,该球的编号为a,将球放回袋中,然后再从袋中随机取一个球,该球的编号为b,求直线ax+by+1=0与圆x2+ y2=
正确答案
见解析。
解析
知识点
在一次抽奖活动中,有a、b、c、d、e、f 共6人获得抽奖的机会。抽奖规则如下:主办方先从6人中随机抽取两人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖。
(1)求a能获一等奖的概率;
(2)若a、b已获一等奖,求c能获奖的概率。
正确答案
(1)
(2)
解析
(1)设“a能获一等奖”为事件A,
事件A等价于事件“从6人中随机取抽两人,能抽到a”.从6人中随机抽取两人的基本事件有(a、b)、(a、c)、(a、d)、(a、e)、(a、f)、(b、c)、(b、d)、(b、e)、(b、f)、(c、d)、(c、e)、(c、f)、(d、e)、(d、f)、(e、f)15个, ………………4分
包含a的有5个,所以,P(A)=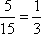
答: a能获一等奖的概率为
(2)设“若a、b已获一等奖,c能获奖”为事件B,
a、b已获一等奖,余下的四个人中,获奖的基本事件有(c,c)、(c、d)、(c、e)、(c、f)、(d,c)、(d、d)、(d、e)、(d、f)、(e,c)、(e、d)、(e、e)、(e、f)、(f,c)、(f、d)、(f、e)、(f、f)16个, ………………11分
其中含有c的有7种,所以,P(B)=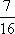
答: 若a、b已获一等奖,c能获奖的概率为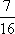
知识点
我市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄(单位:岁)分组:第1组




(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参
加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)请根据频率分布直方图,估计这100名志愿者样本的平均数;
(3)在(1)的条件下,该市决定在这6名志愿者中随机抽取2
名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率。
(参考数据:
正确答案
见解析。
解析
(1)第3组的人数为0.3×100=30, 第4组的人数为0.2×100=20, 第5组的人数为0.1×100=10.
因为第3,4,5组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:第3组:


所以应从第3,4,5组中分别抽取3人,2人,1人.
(2) 根据频率分布直方图,样本的平均数的估计值为:

所以,样本平均数为32.25岁.
(3) 记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,第5组的1名志愿者为C1. 则从6名志愿者中抽取2名志愿者有:
(A1,A2), (A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),
(A3,C1),(B1,B2),(B1,C1),(B2,C1),共有15种.
其中第4组的2名志愿者B1,B2至少有一名志愿者被抽中的有:(A1,B1), (A1,B2), (A2,B1), (A2,B2), (A3,B1), (A3,B2), (B1,B2), (B1,C1), (B2,C1),共有9种
根据古典概型概率计算公式,得
答:第4组至少有一名志愿者被抽中的概率为
知识点
以下茎叶图记录了甲、乙两组各四名工人
正确答案
解析
略
知识点
从





正确答案
解析
略
知识点
扫码查看完整答案与解析