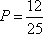随机事件的关系
共288题

· 随机事件的关系

随机事件的关系
共288题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

用计算机产生随机二元数组成区域，对每个二元数组，用计算机计算的值，记“满足 <1”为事件，则事件发生的概率为________.

正确答案

解析

略

知识点

随机事件的关系

题型：简答题

简答题 · 13 分

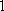
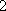
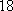
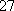
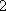
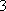
某校高一年级开设研究性学习课程，（）班和（）班报名参加的人数分别是和，现用分层抽样的方法，从中抽取若干名学生组成研究性学习小组，已知从（）班抽取了名同学。

（1）求研究性学习小组的人数；

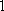
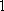
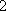
（2）规划在研究性学习的中、后期各安排次交流活动，每次随机抽取小组中名同学发言，求次发言的学生恰好来自不同班级的概率

正确答案

（1）

（2）

解析

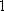
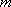
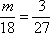
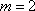
（1）解：设从（）班抽取的人数为，依题意得，所以，

研究性学习小组的人数为，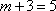

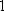
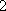
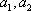
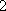
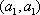
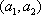
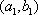
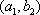
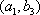
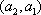
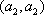
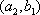
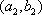
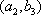
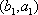
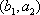
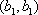
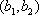
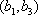
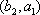
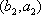
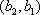
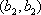
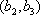
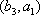
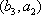
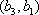
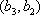
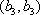
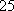
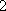
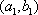
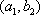
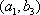
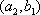
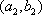
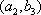
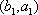
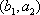
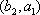
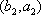
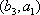
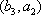
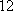
（2）设研究性学习小组中（）班的人为，（）班的人为，

次交流活动中，每次随机抽取名同学发言的基本事件为：

，，，，，

，，，，，共种，

次发言的学生恰好来自不同班级的基本事件为：

，，，，，，，，，

，，，共种，

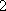
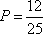
所以次发言的学生恰好来自不同班级的概率为，

知识点

随机事件的关系

题型：简答题

简答题 · 12 分

图(5)是某市2月1日至14日的空气质量指数趋势图，空气质量指数(AQI)小于100表示空气质量优良，空气质量指数大于200表示空气重度污染，某人随机选择2月1日至2月12日中的某一天到达该市，并停留3天。

（1）求此人到达当日空气质量优良的概率;

（2）求此人停留期间至多有1天空气重度污染的概率。

正确答案

见解析。

解析

（1）在2月1日至2月12日这12天中，只有5日、8日共2天的空气质量优良，所以此人到达当日空气质量优良的概率.

（2）根据题意，事件“此人在该市停留期间至多有1天空气重度污染”，即“此人到达该市停留期间0天空气重度污染或仅有1天空气重度污染”

“此人在该市停留期间0天空气重度污染”等价于“此人到达该市的日期是4日或8日或9日”.其概率为，

“此人在该市停留期间仅有1天空气重度污染”等价于“此人到达该市的日期是3日或5日或6日或7日或10日”.其概率为，

所以此人停留期间至多有1天空气重度污染的概率为.P=.

知识点

随机事件的关系

题型：简答题

简答题 · 13 分

是指大气中直径小于或等于微米的颗粒物，也称为可入肺颗粒物，我国标准采用世卫组织设定的最宽限值，即日均值在微克/立方米以下空气质量为一级；在微克/立方米微克/立方米之间空气质量为二级；在微克/立方米以上空气质量为超标。

某城市环保局从该市市区年全年每天的监测数据中随机的抽取天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）。

（1）若从这天的数据中随机抽出天，求至多有一天空气质量超标的概率；

（2）根据这天的日均值来估计一年的空气质量情况，则一年（按天计算）中平均有多少天的空气质量达到一级或二级？

正确答案

（1）

（2）

解析

由茎叶图可知：6天有4天空气质量未超标，有2天空气质量超标………2分

记未超标的4天为，超标的两天为，则从6天抽取2天的所有情况为：

，

基本事件总数为15 ……………………………………………………4分

（1）记“至多有一天空气质量超标”为事件，则“两天都超标”为事件，

易得，所以 ………………9分

（2）天中空气质量达到一级或二级的频率为 ……………11分

，

所以估计一年中平均有天的空气质量达到一级或二级. ………… 13分

（说明：答243天，244天不扣分）

知识点

随机事件的关系

题型：简答题

简答题 · 13 分

一个质地均匀的正方体的六个面上分别标有数字，一个质地均匀的正四面体的四个面上分别标有数字，将这个正方体和正四面体同时抛掷一次，正方体正面向上的数字为，正四面体的三个侧面上的数字之和为。

（1）求事件的概率；

（2）求事件“点满足”的概率。

正确答案

（1）

（2）

解析

（1）由题可知的取值为，的取值为

基本事件空间：

共计24个基本事件 ……………………3分

满足的有共2个基本事件

所以事件的概率为 ……………………7分

（2）设事件B=“点（a,b）满足”

当时，满足

所以满足的有，

所以 ……………………13分

知识点

随机事件的关系

继续学习学习下一知识点

下一知识点 : 随机事件的频率与概率

百度题库 > 高考 > 文科数学 > 随机事件的关系

扫码查看完整答案与解析