- 随机事件的关系
- 共288题
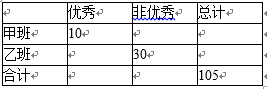
有甲乙两个班进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下列联表。
已知在全部105人中随机抽取1人为优秀的概率为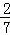
(1)请完成上面的联表;
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班10优秀的学生按2到11进行编号,先后两次抛掷一枚骰子,出现的点数之和为被抽取的序号,试求抽到6号或10号的概率。
参考公式:K2=
概率表
正确答案
见解析。
解析
(1)
(2)根据列联表中的数据,得到k2=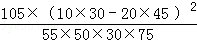
因此有95%的把握认为“成绩与班级有关系”。
(3)设“抽到6或10号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y)。
所有的基本事件有(1,1)、(1,2)、(1,3)、(6,6),共36个。
事件A包含的基本事件有:(1,5)、(2,4)、(3,3)、(4,2)、(5,1)(4,6)、(5,5)、(6、4),共8个
∴P(A)=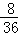
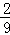
知识点
如图为某个容量为100的样本的频率分布直方图,分组为

正确答案
解析
略
知识点
某校为了研究学生的性别和对待某一活动的态度(支持与不支持)的关系,运用2
附:
正确答案
解析
略
知识点
某高校在2012年的自主招生考试成绩中随机抽以100名学生的

(1)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进

(2)在(1)的前提下,学校决定在

正确答案
见解析。
解析
(1)
由图得,第3组的频率为0.3,故频数为30,第四组的频率为0.2,故频数为20,第5组的频率为0.1,故频数为10。因为第3,4,5组共有60组学生,所以利用分层抽样在60组学生中抽取6名学生,每组分别为
(2)
知识点
一个盒子中装有





(1)若一次抽取


(2)若第一次抽


正确答案
见解析。
解析
(1)设






其中数字之和大于


所以
(2)设

第一次抽1张,放回后再抽取一张卡片的基本结果有:


事件

共
所以所求事件的概率为
知识点
扫码查看完整答案与解析