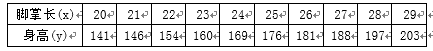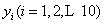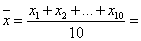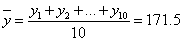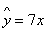- 随机事件的关系
- 共288题
一般来说,一个人脚掌越长,他的身高就越高.现对10名成年人的脚掌长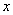
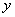
(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,作出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程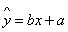
(2)若某人的脚掌长为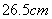
(3)在样本中,从身高180cm以上的4人中随机抽取2人作进一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率。
(参考数据: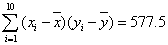
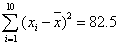
正确答案
见解析。
解析
(1)记样本中10人的“脚掌长”为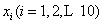

则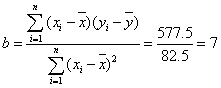
∵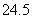
∴
∴
(2)由(20)知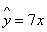
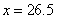
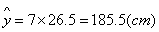
故估计此人的身高为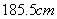
(3)将身高为181、188、197、203(cm)的4人分别记为A、B、C、D,
记“从身高180cm以上4人中随机抽取2人,所抽的2人中至少有1个身高在190cm以上”为事件A,
则基本事件有:(AB)、(AC)、(AD)、(BC)、(BD)、(CD),总数6,
A包含的基本事件有:(AC)、(AD)、(BC)、(BD)、(CD),个数5,
所以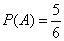
知识点
某校为“市高中数学竞赛”进行选拔性测试,规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰,现有100人参加测试,测试成绩的频率分布直方图如图(4).
(1)求获得参赛资格的人数;
(2)根据频率分布直方图,估算这100名学生
测试的平均成绩;
(3)现在成绩



正确答案
见解析。
解析
(1)由频率分布直方图得,获得参赛资格的人数为:100×(0.0050+0.0045+0.0030)×20=25人。
(2)设100名学生的平均成绩为,则
=[×0.0065+×0.0140+×0.0170+×0.0050+×0.0045+×0.0030]×20=78.4分。
(3) 成绩在




从

其中含有

知识点
某中学高三(1)班有男同学30名,女同学10名,老师按照分层抽样的方法组建了一个
(1)求小组中男、女同学的人数;
(2)从这个小组中先后选出2名同学进行测试,求选出的2名同学中恰有一名女同学的概率。
正确答案
(1)3;1
(2)
解析
(1)设小组中有

所以小组中男、女同学的人数分别为3,1. …………………………………5分
(2)把















所以选出的两名同学中恰有一名女同学的概率为
知识点
盒中装有形状、大小完全相同的7个球,其中红色球4个,黄色球3个,若从中随机取出2个球,则所取出的2个球颜色不同的概率等于 。
正确答案
解析
略
知识点
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户随机抽取3件产品进行检验,若这3件产品中至少有一件次品,就拒收这箱产品;若这3件产品中没有次品,就接收这箱产品,那么这箱产品被用户拒收的概率是 ,(用数字作答)
正确答案
解析
略
知识点
扫码查看完整答案与解析