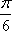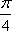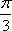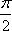导数的加法与减法法则
共610题

· 导数的加法与减法法则

导数的加法与减法法则
共610题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

某单位有职工480人，其中青年职工210人，中年职工150人，老年职工120人，为了了解该单位职工的健康情况，用分层抽样的方法从中抽取样本，若本中的青年职工为7人，则样本容量为。

正确答案

解析

略

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

已知,,且,则向量与夹角的大小为

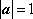
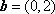
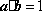
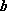
正确答案

解析

略

知识点

导数的加法与减法法则

题型：简答题

简答题 · 14 分

已知N，设函数R.

（1）求函数R的单调区间；

（2）是否存在整数，对于任意N，关于的方程在区间上有唯一实数解，若存在，求的值；若不存在，说明理由。

正确答案

见解析。

解析

解：∵

∴.

方程的判别式.

当时，，，

故函数在R上单调递减；

当时，方程的两个实根为，

则时，；时，；时，；

故函数的单调递减区间为和，

单调递增区间为.

（2）解：存在，对于任意N，关于的方程在区间上有唯

一实数解，理由如下：

当时，，令，解得，

∴关于的方程有唯一实数解.

当时，由，

得.

若，则，

若，则,

若且时，则,

当时，,

∴，故在上单调递减.

∵，

∴方程在上有唯一实数解.

当时，；当时，.

综上所述，对于任意N，关于的方程在区间上有唯一实数解.

∴.

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

正确答案

解析

略

知识点

导数的加法与减法法则

题型：简答题

简答题 · 14 分

已知，函数.

（1）求的单调区间；

（2）当时，证明：方程在区间（2，）上有唯一解；

（3）若存在均属于区间[1，3]的且，使=，证明：。

正确答案

见解析。

解析

（1）函数的定义域，

令得：，令得：

∴函数的单调递减区间为，单调递增区间为

（2）证明：当时，，由（1）知的单调递减区间为，单调递增区间为，

令，则在区间单调递增且，

∴方程在区间（2，）上有唯一解。

（注：检验的函数值异号的点选取并不唯一）

（3）证明：由及（1）的结论知，

从而在上的最大值为（或），

又由知

故，即

从而。

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

若复数在复平面内对应的点在轴负半轴上，则实数的值是（　　）

正确答案

解析

略

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

下列函数中，为偶函数且有最小值的是（）

正确答案

解析

略

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

设上随机地取值，则关于x的方程有实数根的概率为

正确答案

解析

略

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

下列命题中正确的是（）

A如果两条直线都平行于同一个平面，那么这两条直线互相平行

B过一条直线有且只有一个平面与已知平面垂直

C如果一条直线平行于一个平面内的一条直线，那么这条直线平行于这个平面

D如果两条直线都垂直于同一平面，那么这两条直线共面

正确答案

解析

略

知识点

导数的加法与减法法则

题型：简答题

简答题 · 14 分

已知复数，其中，，，是虚数单位，且，。

（1）求数列，的通项公式；

（2）求和：①；②。

正确答案

（1）（2），

解析

解析：（1），，。

由得，………………3分

数列是以1为首项公比为3的等比数列，数列是以1为首项公差为2的等差数列，，，……………………6分

（2）由（1）知，。

①，……10分

②令，（Ⅰ）

将（Ⅰ）式两边乘以3得（Ⅱ）

将（Ⅰ）减（Ⅱ）得。

，.……………………14分

知识点

导数的加法与减法法则

继续学习学习下一知识点

下一知识点 : 导数的乘法与除法法则

百度题库 > 高考 > 文科数学 > 导数的加法与减法法则

扫码查看完整答案与解析