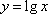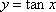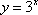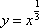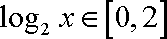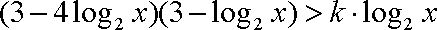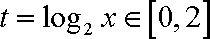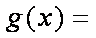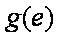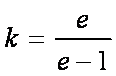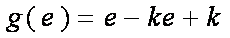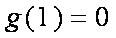- 导数的加法与减法法则
- 共610题
下列函数在其定义域内既是奇函数又是增函数的是
正确答案
解析
略
知识点
已知α、β均为锐角,且
正确答案
解析
知识点
将边长为2的正方形沿对角线




正确答案
解析
略
知识点
已知函数

(1) 求函数

(2) 若函数



(3) 若方程

正确答案
见解析
解析
(1)因为

又


(2)因为





即


又



欲




(3) 原方程等价于


因为当



……………………10分
又

所以当





故

从而当

知识点
已知函数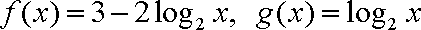
(1)当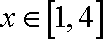
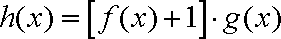
(2)如果对任意的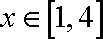
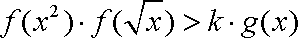
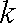
正确答案
见解析
解析
(1)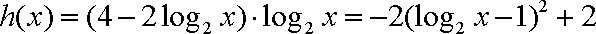
因为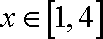

故函数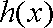
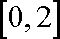
(2)由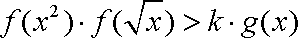
令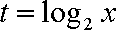
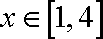
所以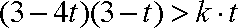
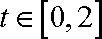

① 当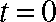
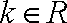
② 当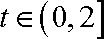
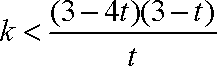
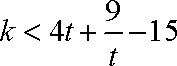
因为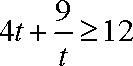
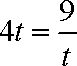
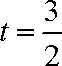
所以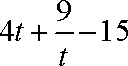
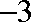
综上,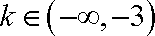
知识点
已知函数
(1)求函数
(2)求函数

正确答案
见解析
解析
解: (1)因为
故
(2)当
故所求的值域为
知识点
已知函数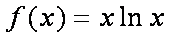
(1)求函数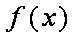
(2)设函数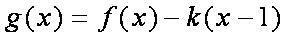
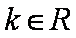
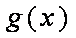
正确答案
见解析
解析
(1)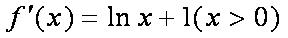
令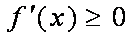
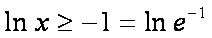
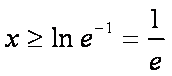
令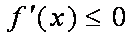
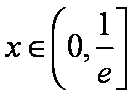
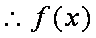
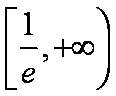


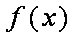
(2)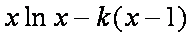
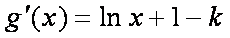
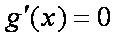
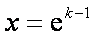
所以,在区间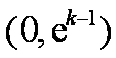
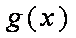
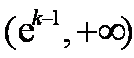
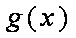
当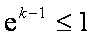
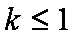
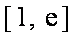
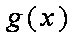
所以,
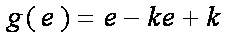
当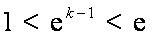
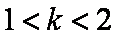
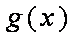
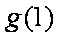

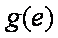
当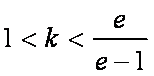
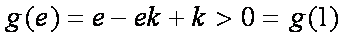
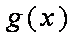
当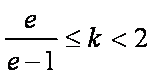
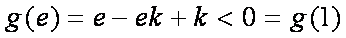
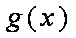
当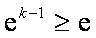
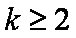
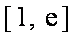
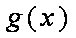
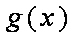
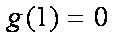
综上,当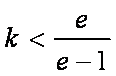
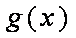
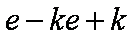
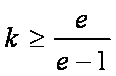
知识点
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点



(1)求

(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米,设花坛的面积与装饰总费用的比为




正确答案
见解析。
解析
(1)设扇环的圆心角为,则

所以
(2)花坛的面积为
装饰总费用为
所以花坛的面积与装饰总费用的比
令

此时
答:当x=1时,花坛的面积与装饰总费用的比最大。
知识点
黑板上有一道解答正确的解三角形的习题,一位同学不小心把其中一部分擦去了,现在只能看到:在△ABC中,角A、B、C的对边分别为n、6、c,已知a=2,…,解得
正确答案
解析
可将选项的条件逐个代入验证。
知识点
已知函数
(1)求
(2)求
(3)求

正确答案
见解析。
解析
(1)

所以最小正周期为
(2) 由 
整理,得

(3)当

故当x=0时,

知识点
扫码查看完整答案与解析