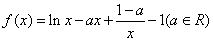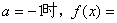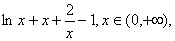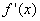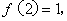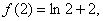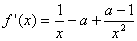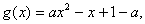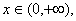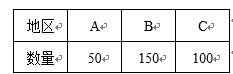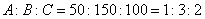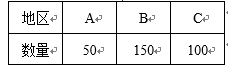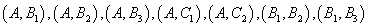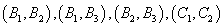- 导数的加法与减法法则
- 共610题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设函数f(x)=alnx+
(1)求b;
(2)若存在x0≥1,使得f(x0)<
正确答案
(1)1
(2)a的取值范围是
解析
(1)f′(x)=
∴f′(1)=a+(1﹣a)×1﹣b=0,解得b=1。
(2)函数f(x)的定义域为(0,+∞),由(1)可知:f(x)=alnx+
∴

①当a

∴函数f(x)在(1,+∞)单调递增,
∴存在x0≥1,使得f(x0)<


解得
②当

则当x∈

当x∈

∴存在x0≥1,使得f(x0)<

而


③若a>1时,f(1)=
综上可得:a的取值范围是
知识点
已知函数
(1)当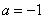
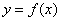
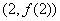
(2)当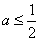
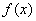
正确答案
见解析。
解析
解:(1) 当
所以
因此,
即 曲线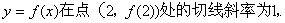
所以曲线
(2)因为 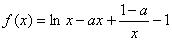
所以 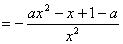
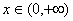

(i)当a=0时,g(x)=-x+1,x∈(0,+∞),
所以 当x∈(0,1)时,g(x)>0,此时f(x)<0,函数f(x)单调递减
(ii)当a≠0时,由
即 ax2-x+1=0, 解得 x1=1,x2=1/a-1
① 当a=1/2时,x1= x2, g(x)≥0恒成立,此时f(x)≤0,函数f(x)在(0,+∞)上单调递减;
② 当0<a<1/2时,1/2-1>1>0
x∈(0,1)时,g(x)>0,此时f(x)<0,函数f(x)单调递减
x∈(1,1/a-1)时,g(x)>0,此时f(x)<o,函数f(x)单调递减
x∈(1/a-1,+∞)时,g(x
③ 当a<0时,由于1/a-1<0,[来源:学。科。网]
x∈(0,1)时,g(x)>0,此时f,(x)<0函数f(x)单调递减;
x∈(1 ,∞)时,g(x)<0此时函数f,(x)<0单调递增。
综上所述:
当a≤ 0 时,函数f(x)在(0,1)上单调递减;
函数f(x)在 (1, +∞) 上单调递增
当a=1/2时,函数f(x)在(0, + ∞)上单调递减
当0<a<1/2时,函数f(x)在(0,1)上单调递减;
函数 f(x)在(1,1/a -1)上单调递增;
函数f(x)在(1/a,+ ∞)上单调递减。
知识点
已知函数f(x)=π(x﹣cosx)﹣2sinx﹣2,g(x)=(x﹣π)

证明:
(1)存在唯一x0∈(0,
(2)存在唯一x1∈
正确答案
见解析。
解析
(1)当x∈(0,
∴f(x)在(0,
又f(0)=﹣π﹣2<0,f(

∴存在唯一x0∈(0,
(2)当x∈[
化简可得g(x)=(x﹣π)

=(π﹣x)

令t=π﹣x,记u(t)=g(π﹣t)=﹣


求导数可得u′(t)=
由(1)得,当t∈(0,x0)时,u′(t)<0,当t∈(x0,
∴函数u(t)在(x0,
由u(

∴函数u(t)在[x0,
函数u(t)在(0,x0)上为减函数,
由u(0)=1及u(x0)<0知存在唯一t0∈(0,x0),使u(t0)=0,
于是存在唯一t0∈(0,
设x1=π﹣t0∈(
∴存在唯一x1∈(
∵x1=π﹣t0,t0<x0,
∴x0+x1>π
知识点
选修4—1:几何证明选讲
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE
.(1)证明:∠D=∠E;
(2)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形。
正确答案
见解析。
解析
。
(1) 由题设知得A、B、C、D四点共圆,所以



所以

(2)设BCN中点为,连接MN,则由MB=MC,知MN⊥BC 所以O在MN上,又AD不是O的直径,M为AD 中点,故OM⊥AD, 即MN⊥AD,所以AD//BC,故







知识点
(1)1证明两角和的余弦公式
2由

(2)已知
正确答案
见解析
解析
(1)①如图,在执教坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为Ox,交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.
则P1(1,0),P2(cosα,sinα)
P3(cos(α+β),sin(α+β)),P4(cos(-β),sin(-β))
由P1P3=P2P4及两点间的距离公式,得
[cos(α+β)-1]2+sin2(α+β)=[cos(-β)-cosα]2+[sin(-β)-sinα]2
展开并整理得:2-2cos(α+β)=2-2(cosαcosβ-sinαsinβ)
∴cos(α+β)=cosαcosβ-sinαsinβ.
②由①易得cos(

sin(α+β)=cos[

=cos(

=sinαcosβ+cosαsinβ
(2)∵α∈(π,),cosα=-
∴sinα=-
∵β∈(,π),tanβ=-
∴cosβ=-
cos(α+β)=cosαcosβ-sinαsinβ
=(-


=
知识点
海关对同时从A,B,C三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如右表所示. 工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
(1)求这6件样品中来自A,B,C各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
正确答案
见解析。
解析
(1)因为工作人员是按分层抽样抽取商品,所以各地区抽取商品比例为:
所以各地区抽取商品数为: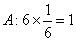
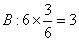
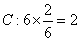
(2)设各地区商品分别为:
基本时间空间
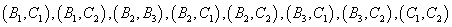
样本时间空间为:
所以这两件商品来自同一地区的概率为: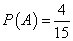
知识点
已知





正确答案
(-4,0)
解析
考查学生函数的综合能力,涉及到二次函数的图像开口,根大小,涉及到指数型函数的平移的单调性,还涉及到简易逻辑中的“或”连接,形式上是小型题,考的确是大思路,分类讨论是这个题的重点。
知识点
阅读右边的程序框图,运行相应的程序,若输入

正确答案
解析
当

当
当

∴
知识点
扫码查看完整答案与解析