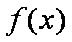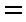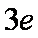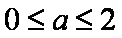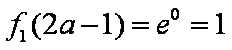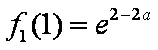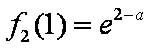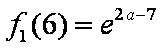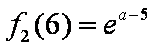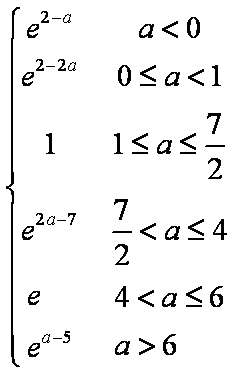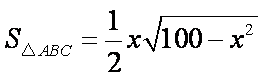- 导数的加法与减法法则
- 共610题
已知函数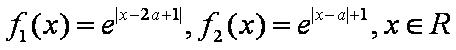
(1)若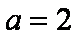
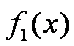
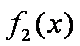
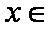
(2)若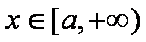
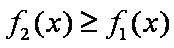
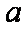
(3)求函数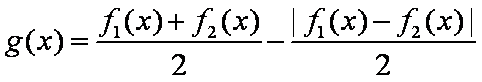
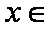
正确答案
见解析
解析
解:(1)因为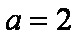
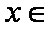

当且仅当x=2时取等号,所以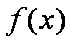
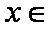
(2)由题意知,当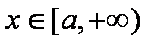
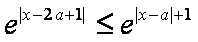
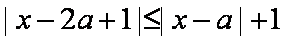
所以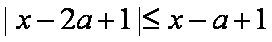
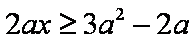
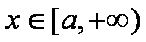
则由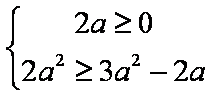
(3) 记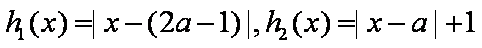
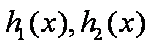
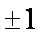
①当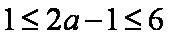
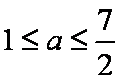
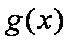
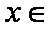
②当a<1时,可知2a-1<a,所以
(ⅰ)当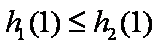
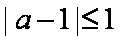
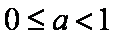
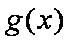
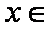
(ⅱ)当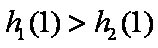
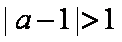
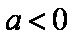
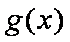
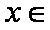
③当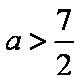
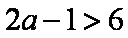
(ⅰ)当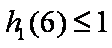
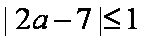
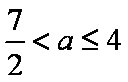
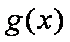
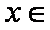
(ⅱ)当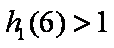
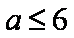
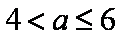
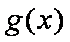
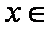
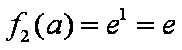
(ⅲ)当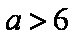
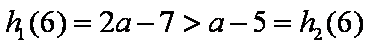
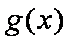
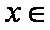
为
综上所述, 函数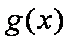
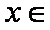
知识点
双曲线


正确答案
解析
由题知

知识点
已知一块半径为









正确答案
见解析。
解析
如图甲,设
则

所以
当且仅当
此时点





[来源:学#科#网]
如图乙,设


所以

设

当







因为
所以选择图乙的方案,截得的直角三角形面积最大,最大值为
知识点
已知函数
(1)设

(2)在




正确答案
见解析。
解析
(1)

由

因为
于是


(2)因为
又因

由余弦定理得
所以
由正弦定理得
所以
知识点
若一个螺栓的底面是正六边形,它的主视图和俯视图如图所示,则它的体积是 ( )
正确答案
解析
该几何体是一个下面为正六棱柱,上面是一个圆柱的组合体,正六棱柱的体积为


知识点
在锐角三角形ABC中,已知角A、B、C所对的边分别为a、b、c,且
(1)若c2=a2+b2—ab,求角A、B、C的大小;
(2)已知向量
正确答案
见解析。
解析
(1)由已知得
(2)
知识点
在斜三角形ABC中,角A,B,C所对的边分别为a,b,c且
(1)求角A;
(2)若
正确答案
见解析
解析
(1)∵ 
又∵ 


∵

∵

(2)∵

即


知识点
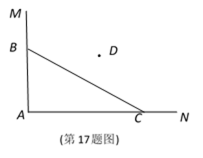
在一个矩形体育馆的一角MAN内(如图所示),用长为a的围栏设置一个运动器材储
存区域,已知B是墙角线AM上的一点,C是墙角线AN上的一点。
(1)若BC=a=10,求储存区域三角形ABC面积的最大值;
(2)若AB=AC=10,在折线MBCN内选一点D,
使DB+DC=a=20,求储存区域四边形DBAC
面积的最大值。
正确答案
见解析
解析
(1)设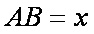
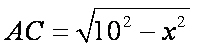
所以

当且仅当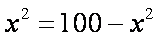
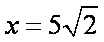
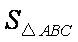
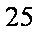
(2)由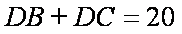
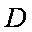
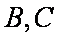
因为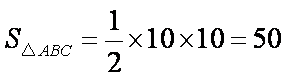
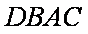
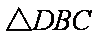
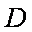
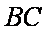
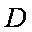
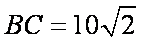
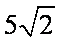
所以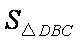
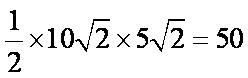
因此,四边形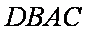
知识点
某商场有四类食品,其中粮食类、植物油类、动物类及果蔬类分别有40种、10种、30种、20 种,现采用分层抽样的方法,从中随机抽取一个容量为20的样本进行食品安全检测,则抽取的动物类食品种数是 。
正确答案
6
解析
抽取比例为


知识点
已知




(1)求
(2)若

正确答案
见解析。
解析
(1)由


代入

由


⑵由

即
所以
由


代入①,整理得
代入

解得

因为

知识点
扫码查看完整答案与解析