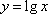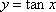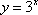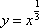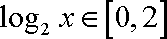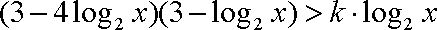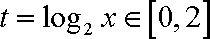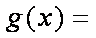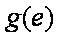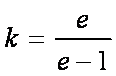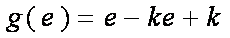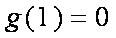- 导数的加法与减法法则
- 共610题
下列函数在其定义域内既是奇函数又是增函数的是
正确答案
解析
略
知识点
将边长为2的正方形沿对角线




正确答案
解析
略
知识点
已知函数

(1) 求函数

(2) 若函数



(3) 若方程

正确答案
见解析
解析
(1)因为

又


(2)因为





即


又



欲




(3) 原方程等价于


因为当



……………………10分
又

所以当





故

从而当

知识点
已知函数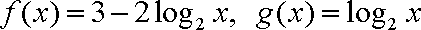
(1)当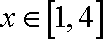
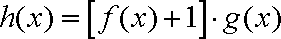
(2)如果对任意的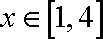
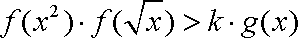
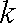
正确答案
见解析
解析
(1)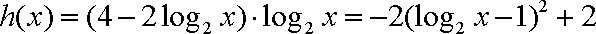
因为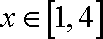

故函数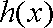
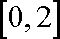
(2)由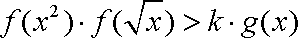
令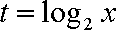
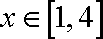
所以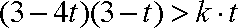
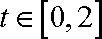

① 当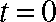
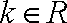
② 当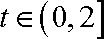
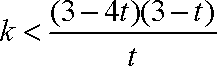
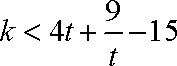
因为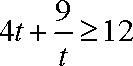
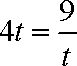
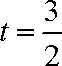
所以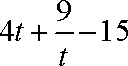
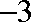
综上,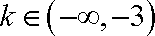
知识点
已知函数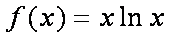
(1)求函数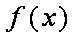
(2)设函数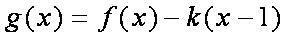
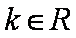
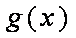
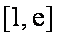
正确答案
见解析
解析
(1)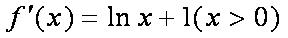
令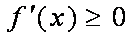
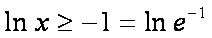
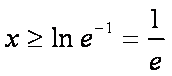
令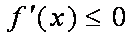
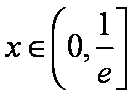
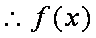
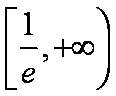


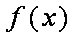
(2)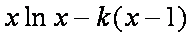
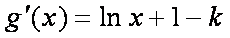
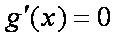
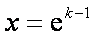
所以,在区间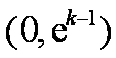
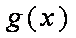
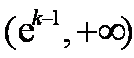
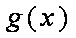
当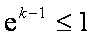
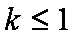
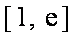
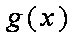
所以,
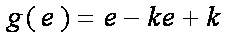
当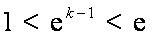
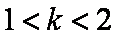
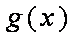
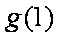

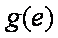
当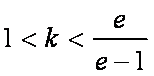
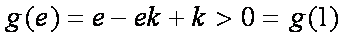
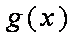
当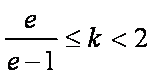
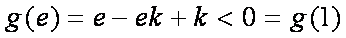
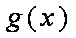
当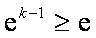
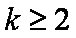
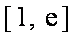
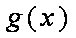
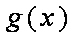
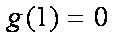
综上,当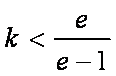
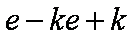
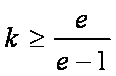
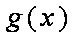
知识点
扫码查看完整答案与解析