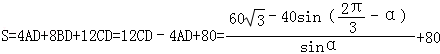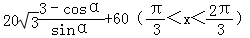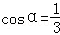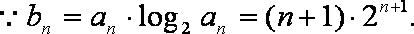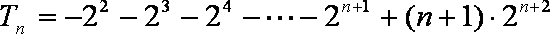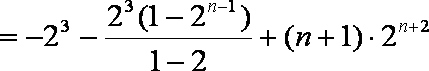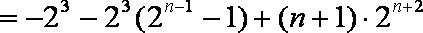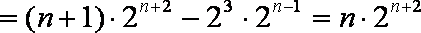导数的加法与减法法则
共610题

导数的加法与减法法则
共610题

热门试卷

题型：简答题

简答题 · 14 分

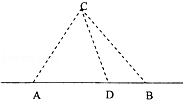
如图，在海岸线l一侧C处有一个美丽的小岛，某旅游公司为方便游客，在l上设立了A、B两个报名点，满足A、B、C中任意两点间的距离为10千米，公司拟按以下思路运作：先将A、B两处游客分别乘车集中到AB之间的中转点D处（点D异于A、B两点），然后乘同一艘游轮前往C岛，据统计，每批游客A处需发车2辆，B处需发车4辆，每辆汽车每千米耗费2元，游轮每千米耗费12元，设∠CDA=α，每批游客从各自报名点到C岛所需运输成本S元。

（1）写出S关于α的函数表达式，并指出α的取值范围；

（2）问中转点D距离A处多远时，S最小？

正确答案

见解析。

解析

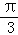
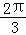
（1）由题在△ACD中，∵∠CAD=∠ABC=∠ACB=，∠CDA=α，∴∠ACD=﹣α。

又AB=BC=CA=10，△ACD中，

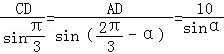
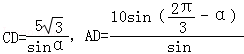
由正弦定理知，得，

∴

（2），令S′=0，得

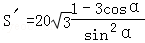
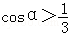
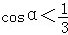
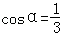
当时，S′＜0；当时，S′＞0，∴当时S取得最小值

此时，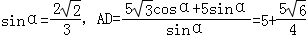

∴中转站距A处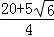千米时，运输成本S最小

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

若向量，其中，设函数，其周期为，且是它的一条对称轴。

（1）求的解析式；

（2）当时，不等式恒成立，求实数a的取值范围。

正确答案

见解析。

解析

（1）………………………………………………………… 2分

……………………………………………………………………5分

∵周期为 ∵………………………………………………………………6分

又∵为其一条对称轴 ∴

∴ 故 …………………………………………………………………7分

∴………………………………………………………………………8分

（2）∵ ∴ ………………………………………………9分

的最小值为…………………………………………………………10分

由恒成立，得…………………………………………………………11分

所以a的取值范围为………………………………12分

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

已知向量

（1）当时，求的值；

（2）设函数，已知在△ABC中，内角A、B、C的对边分别为，若,求的取值范围.

正确答案

见解析。

解析

（1） …………2分

…………6分

（2）

由正弦定理得可得，所以…………………9分

所以--------------------12分

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

已知数列的前n项和为，求一切正整数n，点都在函数的图象上. （1）求数列的通项公式；（2）设，求数列的前n项的和

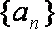
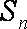
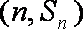
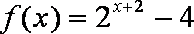
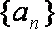
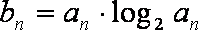
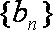
正确答案

见解析。

解析

（2）

①

②

②-①得，

知识点

导数的加法与减法法则

题型：简答题

简答题 · 13 分

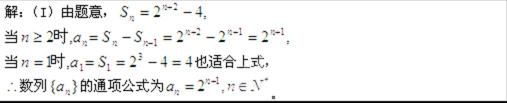
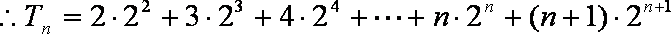
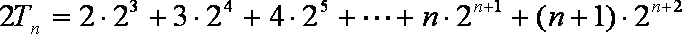
设函数的定义域为R，当时，，且对任意的实数,，有

（1）求；

(2)试判断函数在上是否存在最大值，若存在，求出该最大值，若不存在说明理由；

（3）设数列各项都是正数，且满足，又设，，试比较与的大小.

正确答案

见解析。

解析

（1）令………1分

∵…………………………2分

(2) 又∵ ∴当由＝1得

故对于…………………………3分

设则由已知得 ∴……5分

∴函数在R上是单调递增函数.

∴函数在上存在最大值，f(x)max=f(0)=1…………………………6分

(3) 由得

即

∵函数是R上单调函数. ∴……………………8分

∵数列各项都是正数，∴∴

∴数列是首项，公差为1的等差数列，且.……………10分

∴

而

∵当n＝1时， ∴

当时，

∴ ∴.……………………………………………………13分

知识点

导数的加法与减法法则

继续学习学习下一知识点

下一知识点 : 导数的乘法与除法法则

百度题库 > 高考 > 文科数学 > 导数的加法与减法法则

扫码查看完整答案与解析