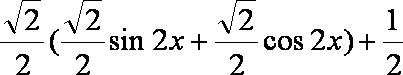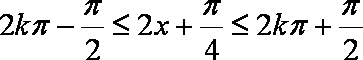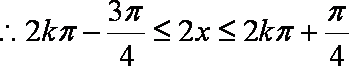- 导数的加法与减法法则
- 共610题
已知函数
(1)若

(2)若

正确答案
见解析。
解析
(1)






















当



当

当

故



即
又

故

所以

知识点
在四边形ABCD中,
正确答案
解析
由











知识点
已知抛物线

正确答案
8
解析
由题设
抛物线方程为

直线过焦点F,联立

知识点
已知平面向量a
(1)若存在实数







(2)根据(1)的结论,试求出函数

正确答案
见解析。
解析
(1


∴
∴

(2)
∵


则
当且仅当


知识点
已知数列




正确答案
2
解析

从上面可以看出
r1=1,r3=2,r5=2,r7=1,r9=1,r11=2,r13=2,r15=1



知识点
如图,已知AF






(1)求证:AC
(2)求三棱锥A
(3)线段EF上是否存在一点M,使得BM
正确答案
见解析
解析
解析:
(1)过C作CN
因为AD


又因为AD




所以AC2+BC2


因为AF


又因为BE



所以AC
(2)因为AF
所以BE

(3)存在,点M为线段EF中点,证明如下: …………9分
在矩形ABEF中,因为点M,N为线段AB的中点,所以四边形BEMN为正方形,
所以BM
因为AF


在直角梯形ABCD中,AD



又CN//AD,所以CN
又BM

又 CN



所以BM
知识点
已知函数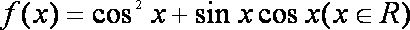
(1)求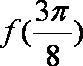
(2)求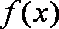
正确答案
见解析。
解析
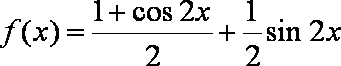
=
=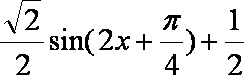
(1)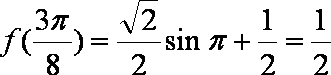
(2)令
即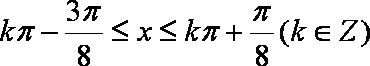
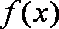
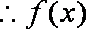
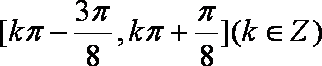
知识点
已知



正确答案
解析
令
如图方程


则
令
在坐标系bot中
联立
联立
解不等式
得:
另解:取
将



再取
因此选“B”
知识点
已知


① 过点

② 过点

③ 过点

④ 过点

则四个结论中正确的个数为( )
正确答案
解析
①错。因为过直线





知识点
若函数





正确答案
解析
知识点
扫码查看完整答案与解析