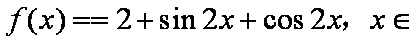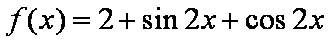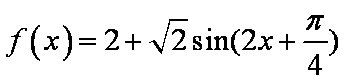- 导数的加法与减法法则
- 共610题
如图,已知三棱锥




(1)求证:

(2)若



正确答案
见解析。
解析
(1)





又





(2)设点












知识点
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建坐标系,已知曲线C: 

(1)写出曲线C和直线l 的普通方程;

正确答案
见解析。
解析
(1)
(2)直线


代入

则有
因为

解得 
知识点
如图,











(1)求证:

(2)若



正确答案
见解析
解析
(1)证明:连接








又






(2)由(1)可知△







由切割线定理得:

知识点
在直角坐标系xOy中,直线l的参数方程为






(1)求

(2)求|

正确答案
见解析
解析
由
得

将直线l的参数方程代入圆C的直角坐标方程,得










又直线l过点,故由上式及参数t的几何意义得
=
知识点
过点P(0,﹣2)的双曲线C的一个焦点与抛物线x2=﹣16y的焦点相同,则双曲线C的标准方程是( )
正确答案
解析
∵抛物线x2=﹣16y的焦点为(0,﹣4)
∴双曲线C的一个焦点坐标为(0,﹣4),
由题意可设双曲线C的标准方程为
∵过点P(0,﹣2)
∴
∴a=2,b=2
∴双曲线C的标准方程是
故选C
知识点
在



(1)求角
(2)若


正确答案
见解析
解析
(1)由已知得
∴


(2)法一:由余弦定理得
∴

解得
又

∴

法二:由正弦定理得
又



∵

∴

知识点
如图,矩形







(1)求证:
(2)求三棱锥
正确答案
见解析
解析
解析:
(1)证明:
∴
又
∴
∴
∴
∴




∴
∴
∴
∴
∴
知识点
已知p:方程x2+mx+1=0有两个不相等的负实根;q:不等式4x2+4(m-2)x+1>0的解集为R,若p或q为真命题,p且q为假命题,求m的取值范围。
正确答案
解析
解析:p为真命题⇔⇒m>2
q为真命题⇔△=[4(m-2)]2-4×4×1<0⇒1<m<3.
∵p或q为真,p且q为假,∴p与q一真一假。
若p真q假,则m>2,且m≤1或m≥3,所以m≥3.
若p假q真,则m≤2,且1<m<3,所以1<m≤2.
综上所述,m的取值范围为{m|1<m≤2,或m≥3}
知识点
已知函数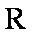
(1)函数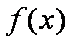
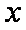
(2)函数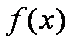
正确答案
见解析
解析
解析:(1)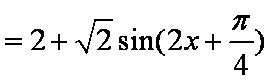
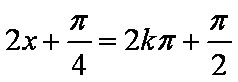
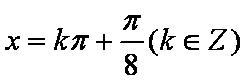
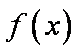
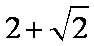
因此,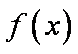
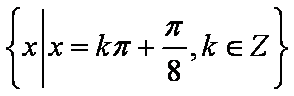
(2)
由题意得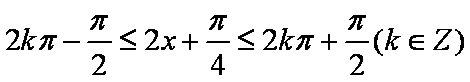
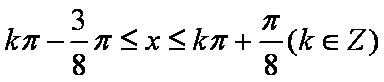
因此,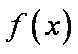
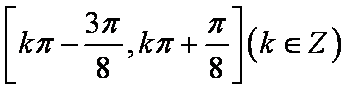
知识点
已知侧棱垂直于底面的三棱柱


(1)证明:
(2)在线段




正确答案
见解析
解析
(1)连结


∵四边形
∴


由题意知
∴

又∵




∵


(2)存在点



连接




∴四边形


∵





知识点
扫码查看完整答案与解析