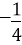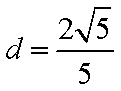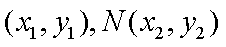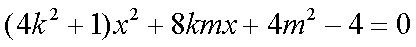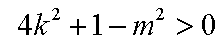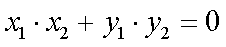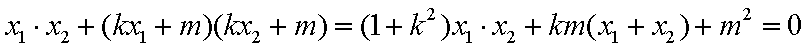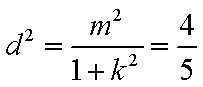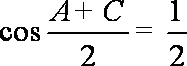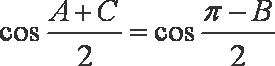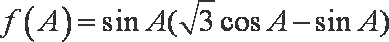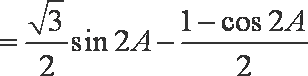- 导数的加法与减法法则
- 共610题
某流感病研究中心对温差与甲型H1N1病毒感染数之间的相关关系进行研究,他们每天将实验室放入数量相同的甲型H1N1病毒和100头猪,然后分别记录了4月1日至4月5日每天昼夜温差与实验室里100头猪的感染数,得到如下资料:
(1)求这5天的平均感染数;
(2)从4月1日至4月5日中任取2天,记感染数分别为



正确答案
(1)10(2)
解析
解析:(1)这5天的平均感染数为
(2)

设满足
则事件A包含的基本事件为
所以


知识点
已知平面上的动点P(x,y)及两个定点A(-2,0),B(2,0),直线PA,PB的斜率分别为K1,K2 且K1K2=
(1)求动点P的轨迹C方程;
(2)设直线L:y=kx+m与曲线 C交于不同两点,M,N,当OM⊥ON时,求O点到直线L的距离(O为坐标原点)
正确答案
(1)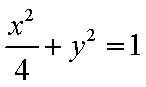
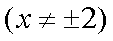
解析
(1)设
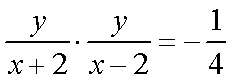
整理得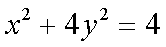
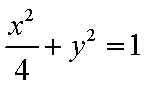
(2)设M
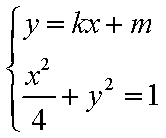
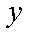
由 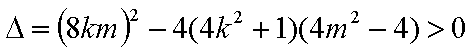
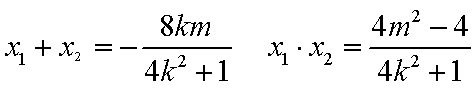
∵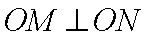
即
∴
∴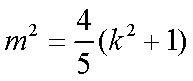
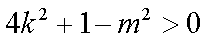
∴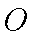
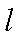
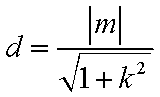
∴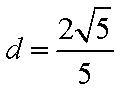
知识点
关于x的方程ex-1-|kx|=0(其中e=2.71828…是自然对数的底数)的有三个不同实根,则k的取值范围是
正确答案
解析
在同一平面直角坐标系中画出函数y=ex-1和y=|kx|的图像,当函数y=ex-1和y=|kx|的图像相切时,设切点为


知识点
如图所示,A、B、C是圆O上的三点,线段CO的延长线与线段BA的延长线交于圆O外的一点D,若

正确答案
解析
解析:










知识点
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=
90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
(1)求证:CD⊥平面PAC;
(2)侧棱PA上是否存在点E,使得BE∥平面PCD?若存在,指出点E的位置并证明,若不存在,请说明理由;
(3)求二面角A-PD-C的余弦值。
正确答案
见解析
解析
因为∠PAD=90°,所以PA⊥AD,又因为侧面PAD⊥底面ABCD,且侧面PAD∩底面ABCD=AD,所以PA⊥底面ABCD,又因为∠BAD=90°,
所以AB,AD,AP两两垂直,分别以AB,AD,AP为x轴,y轴,z轴建立空间直角坐标系,如图,
设AD=2,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,1)。
(1)证明:


所以



又因为AP∩AC=A,所以CD⊥平面PAC,(4分)
(2)设侧棱PA的中点是E,则E(0,0,


设平面PCD的一个法向量是n=(x,y,z),则
因为

所以
所以n•


因为BE⊄平面PCD,所以BE∥平面PCD,(8分)
(3)由已知,AB⊥平面PAD,所以
由(2)知,n=(1,1,2)为平面PCD的一个法向量。
设二面角A-PD-C的大小为θ,由图可知,θ为锐角,
所以cosθ=


即二面角A-PD-C的余弦值为
知识点
在△ABC中,角A、B、C所对的边长分别为a、b、c,且
(1)若a=3,b=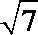
(2)若f(A)=sinA(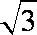
正确答案
见解析。
解析
(1)在△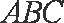

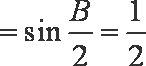
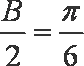
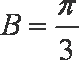
由余弦定理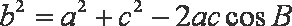
得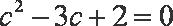
解得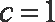
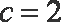
(2)
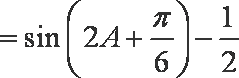
由(1)得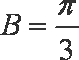
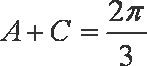
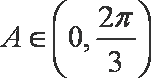
则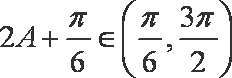
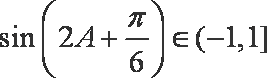
∴
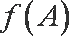
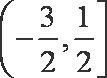
知识点
在


正确答案
答案:
解析
由余弦定理:cosB=
知识点
下列函数既是奇函数,又是增函数的是
正确答案
解析
四个函数中只有函数
知识点
关于函数

正确答案
解析



知识点
已知函数


正确答案
解析
由于




知识点
扫码查看完整答案与解析