- 导数的加法与减法法则
- 共610题
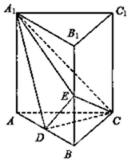
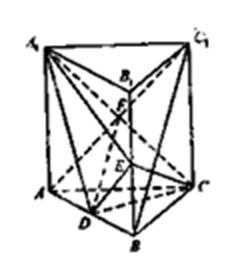
如图,直三棱柱
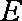
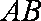
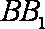
(1)证明: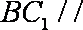
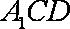
(2)设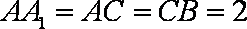
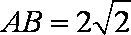
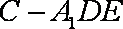
正确答案
见解析
解析
(1)连结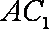


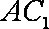
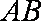
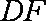
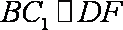
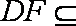
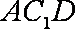


(2)因为三棱柱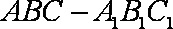
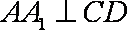
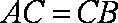
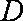
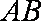

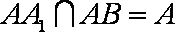
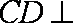

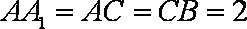
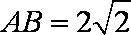
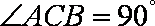
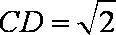
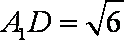

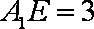

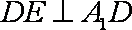

知识点
已知抛物线C:

正确答案
解析
略
知识点
某人在x天观察天气,共测得下列数据:①上午或下午共下雨7次;②有5个下午晴;③有6个上午晴;④ 当下午下雨时上午晴
正确答案
解析
略
知识点
四棱锥P – ABCD中,

(1)求证CE // 平面PAB;
(2)求三棱锥P – ACE体积。
正确答案
见解析
解析
(1)延长DC、AB交于N,连接PN



(2)







知识点
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表:
(1) 完成下面的月工资频率分布直方图(注意填写纵坐标);
(2)
(3) 若从月工资在

正确答案
见解析。
解析
(1)如图
(2)
即该单位员工月平均工资估计为4300元.
(3)由上表可知:月工资在

(甲,乙),(甲,A),(甲,B),(甲,C),(甲,D),
(乙,A),(乙,B),(乙,C),(乙,D),
(A,B),(A,C),(A,D),
(B,C),(B,D),
(C,D)
其中月工资差不超过1000元,即为同一组的有(甲,乙),(A,B),(A,C),(A,D),(B,C),(B,D),(C,D)共7组,
∴所求概率为
知识点
已知


(1)当

(2)设




正确答案
见解析。
解析
(1)
令







(2)因为


所以
知识点
若满足条件AB=


正确答案
解析
若满足条件的三角形有两个,则应



知识点
已知数列




(1)求数列
(2)设



正确答案
见解析
解析
(1)由题设知

由
两式作差得
所以

可见,数列



(2)


知识点
已知P是圆M:x2+y2+4x+4-4m2=0(m>0且m≠2)上任意一点,点N的坐标为(2,0),线段NP的垂直平分线交直线MP于点Q,当点P在圆M上运动时,点Q的轨迹为C。
(1)求出轨迹C的方程,并讨论曲线C的形状;
(2)当m=时,在x轴上是否存在一定点E,使得对曲线C的任意一条过E的弦AB,
正确答案
见解析
解析
(1)m>2,
M<2,
(2)由(1)曲线C为
设

则
解得

下证
设过点E




则


同理可得E
综上得定点为E
知识点
已知函数

(1) 当a=1时,求函数

(2) 求
(3)若存在两不等实根

正确答案
见解析。
解析
(1)当a=1时,

所以切线方程为
(2)
①当


所以





(3)由


令







知识点
扫码查看完整答案与解析