- 导数的加法与减法法则
- 共610题
在△






正确答案
解析
因为




根据余弦定理有



所以
知识点
下列几何体各自的三视图中,有且仅有两个视图相同的是( )
正确答案
解析
对于②,其正视图与侧视图都是等腰三角形,符合题意;对于④,其正视图与侧视图都是等腰三角形,符合题意;另外两个都不符合题意,故选D.
知识点
设定义域为R的函数


正确答案
解析
代入检验,当





有3个不同实根,





知识点


正确答案
解析

知识点
如图所示是一个几何体的三视图,则该几何体的体积为
正确答案
解析
由题意可知,该几何体为一个四棱锥,底面面积为

知识点
如图,在平行四边形





(1)求证:

(2)当


正确答案
见解析
解析
(1)在
∵

又


∴
(2)设E点到平面ABCD距离为

由(I)知
当
∵


∴
∴当


此时


在
在Rt△ADE中,
∵




∴

综上,


知识点
动点



(1)求
(2)过点



正确答案
见解析
解析
(1)由题意得, 
化简得, 


(2)若存在点E(t,0)满足题设条件.并设M(x1,y1)、N(x2,y2),
当
当


所以
根据题意,x轴平分∠MEN,则直线ME、NE的倾斜角互补,即KME+KNE=0。……8分
设E(t,0),则有
又k≠0,所以
又k≠0,所以



将
综上,存在定点E(2,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等。……………12分
知识点
某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示。
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
正确答案
见解析。
解析
(1)由题可知,第2组的频数为

(频率分布直方图略).
(2)因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组分别为,第3组:

第5组:
(3)设第3组的3位同学为



其中第4组的2位同学为
共9种。
所以其中第4组的2位同学为
知识点
已知函数
(1)当

(2)若
①求实数
②证明:
正确答案
见解析
解析
(1)


令


在



最大值



(2) ①

化为
设切点为







解法二.


化为

由

在


在


当


从而
②由①知,当
必有




令




即
知识点
如图,正方形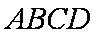
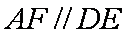
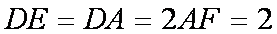
(1)求证: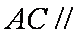
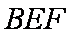
(2)求点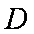
正确答案
见解析。
解析
(1)证明:设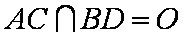
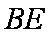
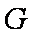
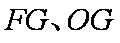
则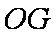
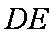
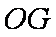
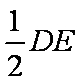
∵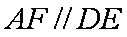
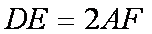
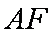
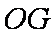
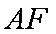
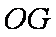
∴四边形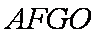
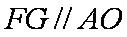
∵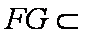
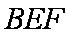
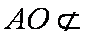
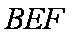
∴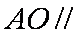
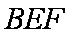
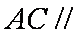
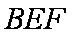
(2)在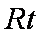
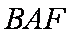
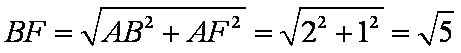
在
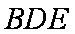

在直角梯形
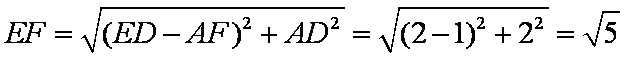
所以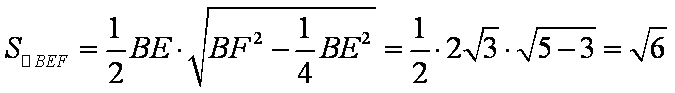

由于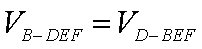
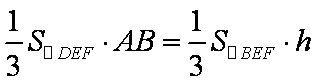
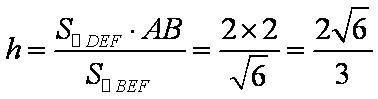
即点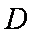
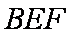
知识点
扫码查看完整答案与解析