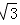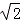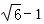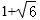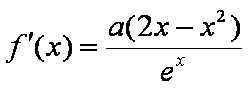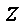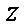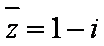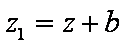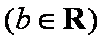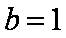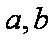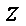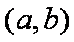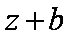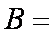- 导数的加法与减法法则
- 共610题
已知函数

则实数
正确答案
0<b<
解析
略
知识点
△ABC中,角A,B,C所对的边分别为a,b,c,若C=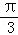
正确答案
解析
∵a=2,c=3,∠C=60°,
∴根据余弦定理得:c2=a2+b2﹣2ab•cosC
9=4+b2﹣2b,
则b=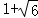
故选D。
知识点
在正项数列




(1)求数列
(2)求数列


正确答案
见解析。
解析
(1)求导得





由


(2)

①-②得,

知识点
已知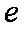
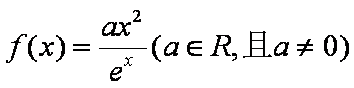
(1)求函数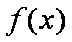
(2)当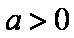
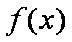

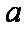
正确答案
见解析。
解析
(1)函数的定义域为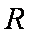
当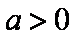
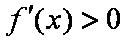
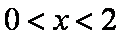
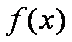
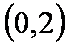
当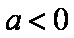
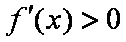
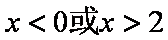
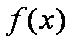
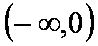
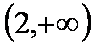
(2)由(1)可知,当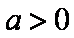
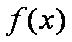
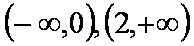
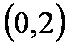
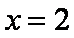
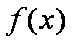
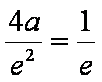
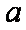
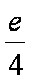
知识点
已知点




正确答案
解析
略
知识点
已知在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,且满足AD⊥AB,BC∥AD,AD=16,AB=8,BB1=8,E,F分别是线段A1A,BC上的点。
(1)若A1E=5,BF=10,求证:BE∥平面A1FD.
(2)若BD⊥A1F,求三棱锥A1-AB1F的体积。
正确答案
见解析
解析
解析:(1)过E作EG∥AD交A1D于G,连接GF.

∵BF∥AD,EG∥AD,∴BF∥EG.
∴四边形BFGE是平行四边形。
∴BE∥FG
又FG⊂平面A1FD,BE⊄平面A1FD,
∴BE∥平面A1FD. …………4分
(2)∵在直四棱柱ABCDA1B1C1D1中,A1A⊥平面ABCD,BD⊂平面ABCD,∴A1A⊥BD.
由已知,BD⊥A1F,AA1∩A1F=A1,
∴BD⊥平面A1AF.∴BD⊥AF
∵梯形ABCD为直角梯形,且满足AD⊥AB,BC∥AD,
∴在Rt△BAD中,tan∠ABD=
在Rt△ABF中,tan∠BAF=
∵BD⊥AF,∴∠ABD+∠BAF=
∴
∵在直四棱柱ABCDA1B1C1D1中,A1A⊥平面ABCD,∴平面AA1B1B⊥平面ABCD,
又平面ABCD∩平面AA1B1B=AB,∠ABF=90°,
∴FB⊥平面AA1B1B,即BF为三棱锥FA1B1A的高,…………10分
∵∠AA1B1=90°,AA1=BB1=8,A1B1=AB=8,
∴S△AA1B1=32.
∴V三棱锥A1AB1F=V三棱锥FA1B1A=×S△AA1B1×BF=
知识点
关于复数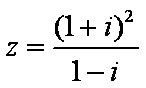
正确答案
解析
由题可知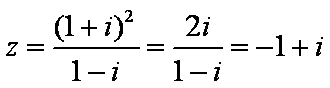
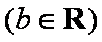
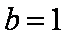
知识点
已知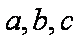
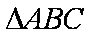
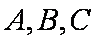
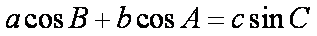
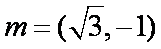
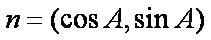
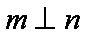
正确答案
解析
由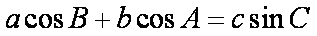
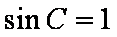
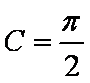
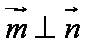
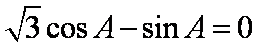
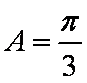
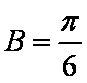
知识点
已知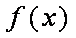
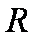
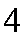
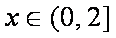
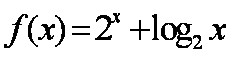
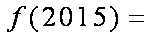
正确答案
解析
略
知识点
为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000株的生长情况进行研究,现采用分层抽样方法抽取50株作为样本,统计结果如下:
(1) 现采用分层抽样的方法,从该样本所含的圆粒玉米中取出6株玉米,再从这6株玉米中随机选出2株,求这2株之中既有高茎玉米又有矮茎玉米的概率;
(2)根据对玉米生长情况作出的统计,是否能在犯错误的概率不超过0.050的前提下认为玉米的圆粒与玉米的高茎有关?(下面的临界值表和公式可供参考:


正确答案
(1)
解析
(1) 依题意,取出的6株圆粒玉米中含高茎2株,记为


其中满足题意的共有

(2)根据已知列联表:
所以
又
知识点
扫码查看完整答案与解析