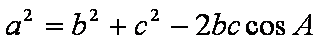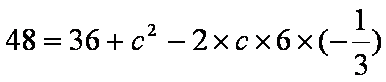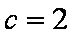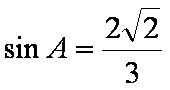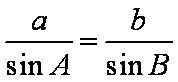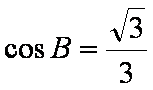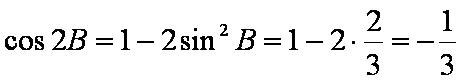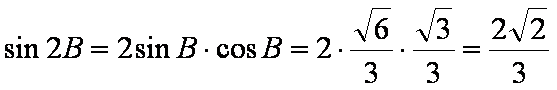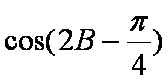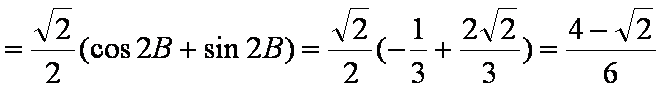- 导数的加法与减法法则
- 共610题
设


正确答案
解析
知识点
在△ABC中,角A,B,C的对边分别为a,b,c,且
(1)求角B的大小;
(2)已知

正确答案
见解析
解析
解:(1)

∵

∴

(2)

∴


而

知识点
已知
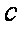
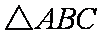
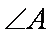
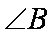
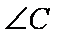
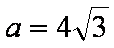
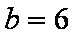
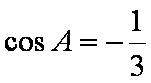
(1)求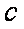
(2)求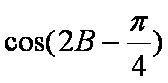
正确答案
见解析
解析
(1)在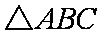
即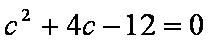
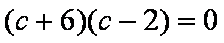
(2)由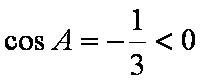
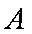
在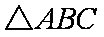
则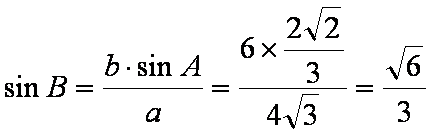
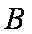
所以
知识点
若实数m、n满

正确答案
解析




因为


当


另解:设
∴


∴



知识点
设函数
(1)求
(2)设函数



正确答案
见解析
解析
解:
(1)解:因为


当



当

所以


(2) 令

根据题意,当

所以
①当


所以


②当


所以


③当




于是“


即


综上所述,

知识点
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=
(1)求证:平面PBC⊥平面ABC;
(2)求二面角A-PB-C的正切值。
正确答案
见解析
解析
(1)
设D为BC的中点,连结AD,DP.
因为AD⊥AC,所以DA=DB=DC.
因为PA=PB=PC,所以△PAD≌△PBD≌△PCD,
所以∠PDA=∠PDB=∠PDC=90°,
即PD⊥平面ABC
因为PD
所以平面PBC⊥平面ABC
(2)证明:过A作AE⊥BC于E,过E作EG⊥PB于G,连结AG.
由(1) 平面PBC⊥平面ABC,且平面PBC∩平面ABC=BC,
所以AE⊥平面PBC,∴AE⊥PB,
又EG⊥PB,且AE,EG
所以PB⊥平面AEG,
又AG
所以∠AGE即为二面角A-PB-C的平面角.
在Rt△ABC中,AB=


在等腰△PBC中,PB=3,AC=2,可得sin∠PBC=

所以,在Rt△AEG中,tan∠AGE=
即二面角A-PB-C的正切值为
知识点
已知数列



(1)求数列
(2)若数列


正确答案
见解析。
解析
(1)∵
∵

数列

当
当
∴
(2)

∵
∴
知识点
如图,在五面体


(1)求证:

(2)若




正确答案
见解析
解析
(1)证明:
(2)
又
过点










取











知识点
甲、乙两名同学在5次数学测验中的成绩统计如茎叶图所示,则甲、乙两人5次数学测验的平均成绩依次为 。
正确答案
83;84
解析
根据茎叶图甲在5次数学测验中的成绩72,74,88,85,96,
即甲同学成绩的平均数是(72+74+88+85+96)=83,
乙同学在5次数学测验中的成绩77,79,81,90,93,
即乙同学成绩的平均数是(77+79+81+90+93)=84,
知识点
已知动点P到直线l:x+4=0的距离与它到点M(2,0)的距离之差为2,记点P的轨迹为曲线C。
(1)求曲线C的方程;
(2)问直线l上是否存在点Q,使得过点Q且斜率分别为k1,k2的两直线与曲线C相切,同时满足k1+2k2=0,若存在,求出点Q的坐标;若不存在,请说明理由。
正确答案
见解析
解析
(1)根据抛物线定义,曲线


所以
故曲线

(2)设


联立

因为相切,故

所以
因为


又因为

故存在点



且满足
知识点
扫码查看完整答案与解析