- 导数的加法与减法法则
- 共610题
设函数
(1)求函数

(2)求
(3)若




正确答案
见解析
解析
解:(1)

函数

(2)
若



若




所以,


(3)由于
故当

令
函数

所以



设此零点为





所以,



所以,

故整数
知识点
设等差数列 



正确答案
解析
∵

知识点
函数
正确答案
1
解析
略
知识点
规定记号“



正确答案
解析
根据运算有
知识点
设函数f(x)是定义在R上的周期为2的偶函数,当x∈[0,1]时,f(x)=x+l,则f(
正确答案
解析
因为函数f(x)是定义在R上的周期为2的偶函数,所以
知识点
已知a为常数,且a≠O,函数f(x)=ax+axlnx+2.
(1)求函数f(x)的单调区间;
(2)当a=1时,若直线y=t与曲线y=f(x)(z∈[
正确答案
见解析。
解析
(1)

因为a≠0,故:
①当a>0时,由f′(x)>0得x>1,由f′(x)<0得0<x<1;
②当a<0时,由f′(x)>0得0<x<1,由f′(x)<0得x>1.
综上,当a>0时,函数f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1);
当a<0时,函数f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞),
(2)当a=1时,f(x)=-x+2+xlnx,f′(x)=lnx.
由(1)可得,当x在区间
又

∵直线y=t与曲线y=f(x)
∴t的取值范围是
知识点
函数f(x)=2lnx-x2的单调递增区间是
正确答案
单调递增区间为
解析
函数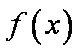
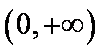

∵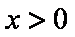
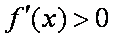
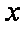
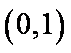
故函数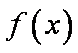
知识点
已知函数



正确答案
解析
略
知识点
双曲线
正确答案
解析
因为a=3,b=4,c=5,所以双曲线

知识点
已知




正确答案
解析
设




可得 



再由 0≤θ≤π可得 θ=
知识点
扫码查看完整答案与解析