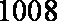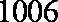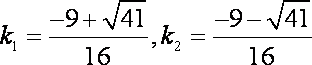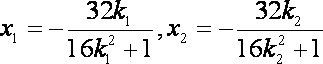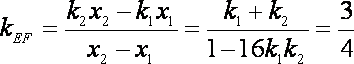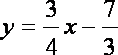- 导数的加法与减法法则
- 共610题
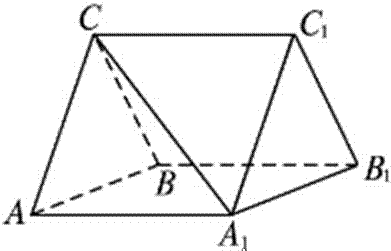
20.如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C=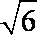
正确答案
见解析。
解析
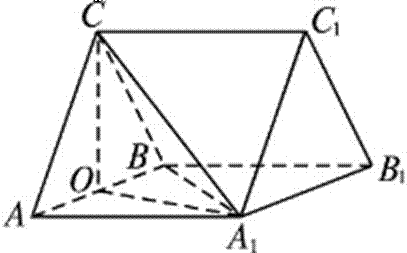
(1)证明:取AB的中点O,连结OC,OA1,A1B.
因为CA=CB,
所以OC⊥AB.
由于AB=AA1,∠BAA1=60°,
故△AA1B为等边三角形,
所以OA1⊥AB.
因为OC∩OA1=O,所以 AB⊥平面OA1C.
又A1C⊂平面OA1C,故AB⊥A1C.
(2)解:由题设知△ABC与△AA1B都是边长为2的等边三角形,
所以OC=OA1=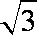
又A1C=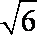
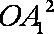
故OA1⊥OC.
因为OC∩AB=O,所以OA1⊥平面ABC,OA1为三棱柱ABC-A1B1C1的高.
又△ABC的面积S△ABC=
知识点
2.若角


正确答案
解析
因为角


所以
知识点
19.在某学校组织的一次篮球总投篮训练中,规定每人最多投3次;在








(1)求
(2)求随机变量

(3)试比较该同学选择在
正确答案
见解析。
解析
(1)由题设知,“

(2)根据题意
因此
(3)用




则

即该同学选择都在


知识点
15.已知偶函数f(x)满足f(x+1)=-
正确答案
解析
略
知识点
6.已知x、y满足约束条件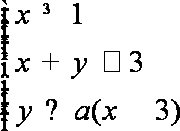
正确答案
解析
先画出可以确定的可行域,再根据含参数a的直线过定点(0,3),考虑该直线与直线x=1交于点
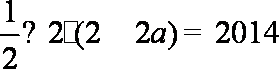
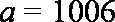
知识点
20.如图,已知圆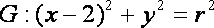
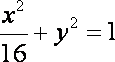
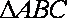
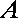
(1)求圆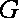
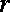
(2)过点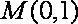
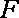
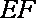
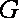
正确答案
见解析。
解析
(1)设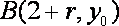
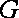

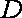
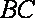
由

即
而点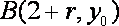
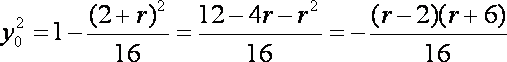
由①、②式得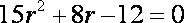
解得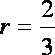
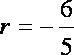
(2)设过点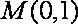

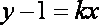
则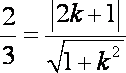
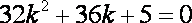
解得
将③代入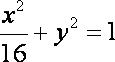
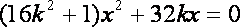
则异于零的解为
设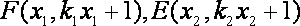
则直线的斜率为:
于是直线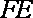
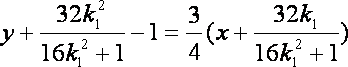
则圆心(2,0)到直线
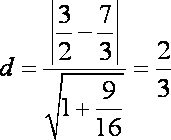
知识点
16.设数列



(1)求


(2)已知





正确答案
见解析。
解析
(1)由题设知{an}是首项为1,公比为3的等比数列,
所以an=3n-1,Sn=

(2)b1=a2=3,b3=1+3+9=13,b3-b1=10=2d,
所以公差d=5,
故T20=20×3+
知识点
18.如图,已知四棱柱


(1)求证:
(2)求证:AC∥平面
正确答案
见解析。
解析
(1)因为底面






(2)设






则








且









所以

知识点
21.已知二次函数


(1)如果


(2)如果
正确答案
见解析。
解析
(1)由




(2)由




即


知识点
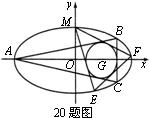
21.已知如图,在平面直角坐标系xoy中,点B

(Ⅰ)求出椭圆C的方程;
(Ⅱ)当直线PA平分FB时,求k的值;
(Ⅲ)当k=2时,求点P到直线AC的距离;
(Ⅳ)是否存在正实数k使
正确答案
见解析。
解析
(Ⅰ)因为椭圆C的长轴长为4,点B



(Ⅱ)由题意可知F为


(Ⅲ)当k=2时,直线l的方程为

解得P点为




(Ⅳ)存在正实数k使

可得




所以
因为k(k>0),当且仅当


知识点
扫码查看完整答案与解析