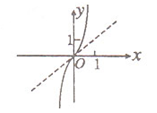
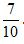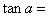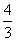- 导数的加法与减法法则
- 共610题
下图是某算法的程序框图,则程序运行后输出的结果是____.
正确答案
27
解析
由框图的顺序,s=0,n=1,s=(s+n)n=(0+1)*1=1,n=n+1=2,依次循环
S=(1+2)*2=6,n=3,注意此刻3>3仍然是否,所以还要循环一次
s=(6+3)*3=27,n=4,此刻输出,s=27.
知识点
已知过抛物线




(1)求该抛物线的方程;
(2)



正确答案
(1) 
解析
(1)直线AB的方程是
所以:

抛物线方程为:
(2)、由p=4,




设





知识点
提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆 /千米)的函数,当桥上的车流魔都达到200辆 /千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆 /千米时,车流速度为60千米/小时,研究表明:当
(1) 当
(2) 当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
正确答案
见解析
解析
(1)由题意:当0≤x≤20时,v(x)=60,当20≤x≤200时,设v(x)=ax+b,
再由已知得
故函数v(x)的表达式为v(x)=
(2)依题意并由(1)可得f(x)=
当0≤x≤20时,f(x)为增函数,故当x=20时,其最大值为60×20=1 200;
当20≤x≤200时,f(x)=



当且仅当x=200-x,即x=100时,等号成立.
所以,当x=100时,f(x)在区间[20,200]上取得最大值
综上,当x=100时,f(x)在区间[0,200]上取得最大值
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3 333辆/小时
知识点
在



(1)求
(2)若

正确答案
(1) 
解析
(1)由 
及:

(2)由

正弦定理:
知识点
某饮料公司对一名员工进行测试以便确定其考评级别,公司准备了两种不同的饮料共5
杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工
一一品尝后,从5杯饮料中选出3杯A饮料,若该员工3杯都选对,则评为优秀;若3
杯选对2杯,则评为良好;否则评为及格,假设此人对A和B两种饮料没有鉴别能力。
(1)求此人被评为优秀的概率;
(2)求此人被评为良好及以上的概率。
正确答案
(1) 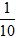
解析
(1)员工选择的所有种类为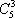
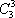
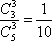
(2)员工选择的所有种类为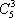
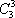
:3杯选中2杯共有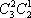

知识点
已知函数f(x)=(ax2+bx+c)ex在[0,1]上单调递减且满足f(0)=1,f(1)=0.
(1)求a的取值范围;
(2)设g(x)=f(x)-f′(x),求g(x)在[0,1]上的最大值和最小值。
正确答案
(1) 0≤a≤1 ;(2) 则当

解析
(1)由f(0)=1,f(1)=0得c=1,a+b=-1,
则f(x)=[ax2-(a+1)x+1]ex,f′(x)=[ax2+(a-1)x-a]ex,依题意须对于任意x∈(0,1),有f′(x)<0.
当a>0时,因为二次函数y=ax2+(a-1)x-a的图像开口向上,
而f′(0)=-a<0,所以须f′(1)=(a-1)e<0,即0<a<1;
当a=1时,对任意x∈(0,1)有f′(x)=(x2-1)ex<0,f(x)符合条件;
当a=0时,对于任意x∈(0,1),f′(x)=-xex<0,f(x)符合条件;
当a<0时,因f′(0)=-a>0,f(x)不符合条件。
故a的取值范围为0≤a≤1.
(2)因g(x)=(-2ax+1+a)ex,g′(x)=(-2ax+1-a)ex,
当a=0时,g′(x)=ex>0,g(x)在x=0上取得最小值g(0)=1,在x=1上取得最大值g(1)=e.
当a=1时,对于任意x∈(0,1)有g′(x)=-2xex<0,g(x)在x=0取得最大值g(0)=2,在x=1时取得最小值g(1)=0.
当0<a<1时,由g′(x)=0得
①若

②若



则当
当
知识点
函数f(x)=sin(x-
正确答案
解析
函数f(x)=sin(x-





知识点
若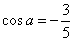
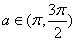
正确答案
解析
因为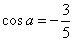
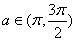
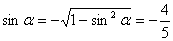
所以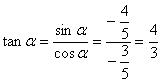
知识点
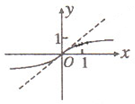
函数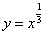
正确答案
解析
选B 取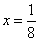
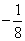
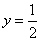
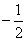
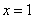
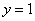
知识点
某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件。为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n=______
正确答案
解析
n = a + b + c=13.
知识点
扫码查看完整答案与解析