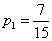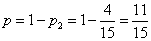- 导数的加法与减法法则
- 共610题
已知a,b是单位向量,a·b=0.若向量c满足|c-a-b|=1,则|c|的最大值为_______
正确答案
解析

知识点
已知集合

正确答案
解析

知识点
已知

正确答案
6
解析

又

知识点
设复数z满足

正确答案
1
解析
略
知识点
如图,已知椭圆C1的中心在原点O,长轴左、右端点M,N在x轴上,椭圆C2的短轴为MN,且C1,C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点按纵坐标从大到小依次为A,B,C,D。
(1)设


(2)当e变化时,是否存在直线l,使得BO∥AN,并说明理由。
正确答案
(1) 
解析
(1)因为C1,C2的离心率相同,故依题意可设
设直线

当

(2)t=0时的l不符合题意.
解得
因为
所以当
当
知识点
如图,等边三角形OAB的边长为
(1)求抛物线E的方程;
(2)设动直线l与抛物线E相切于点P,与直线y=-1相交于点Q,证明以PQ为直径的圆恒过y轴上某定点。
正确答案
见解析
解析
方法一:(1)依题意,
设B(x,y),则x=|OB|sin30°=
y=|OB|·cos 30°=12。
因为点B(

故抛物线E的方程为x2=4y。
(2)由(1)知

设P(x0,y0),则x0≠0,且直线l的方程为y-y0=


由
所以Q(
设M(0,y1),令

由于


由

即(y12+y1-2)+(1-y1)y0=0。(*)
由于(*)式对满足
所以
解得y1=1。
故以PQ为直径的圆恒过y轴上的定点M(0,1)。
方法二:(1)同方法一。
(2)由(1)知

设P(x0,y0),则x0≠0,且直线l的方程为
y-y0=


由
所以Q(
取x0=2,此时P(2,1),Q(0,-1),以PQ为直径的圆为(x-1)2+y2=2,交y轴于点M1(0,1)或M2(0,-1);取x0=1,此时P(1,





故若满足条件的点M存在,只能是M(0,1)。
以下证明点M(0,1)就是所要求的点。
因为




故以PQ为直径的圆恒过y轴上的定点M
知识点
某住宅小区计划植树不少于100棵,若第一天植2棵,以后每天植树的棵树是前一天的2倍,则需要的最少天数n(n∈N*)等于() 。
正确答案
6
解析
直接计算2+4+8+16+32+64=128得n=6, 或解
知识点
已知

正确答案
解析
略
知识点
设函数
(1)讨论
(2)若






正确答案
见解析
解析
(1)
令
(1) 当

(2) 当



(3) 当

当








(2)由(1)知,
因为
又由(1)知,
若存在



再由(I)知,函数





知识点
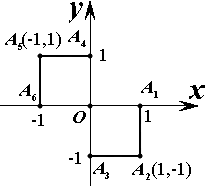
小波已游戏方式决定是去打球、唱歌还是去下棋。游戏规则为以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记住这两个向量的数量积为X,若X>0就去打球,若X=0就去唱歌,若X<0就去下棋。
(1)写出数量积X的所有可能取值
(2)分别求小波去下棋的概率和不去唱歌的概率
正确答案
见解析
解析
(1) x 的所有可能取值为-2 ,-1 ,0, 1。
(2)数量积为-2的只有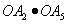
数量积为-1的有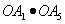
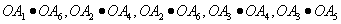
数量积为0的有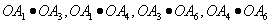
数量积为1的有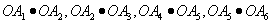
故所有可能的情况共有15种。
所以小波去下棋的概率为
因为去唱歌的概率为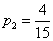
知识点
扫码查看完整答案与解析