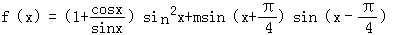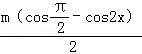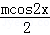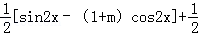- 导数的加法与减法法则
- 共610题
5.已知

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数f(x)=(1+cotx)sin2x+msin(x+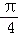
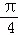
(1)当m=0时,求f(x)在区间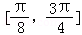
(2)当tana=2时,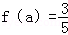
正确答案
解:(1)当m=0时,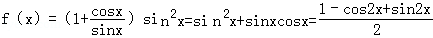
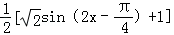
由已知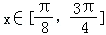
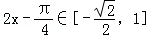
从而得:f(x)的值域为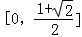
(2)因为
=sin2x+sinxcosx+
=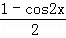
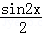
=
所以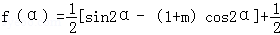
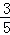
当tanα=2,得: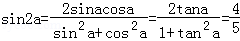
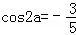
代入①式,解得m=﹣2.
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)当f(x)的定义域为
(2)试问对定义域内的任意x,f(2a﹣x)+f(x)的值是否为一个定值?若是,求出这个定值;若不是,说明理由;
(3)设函数g(x)=x2+|(x﹣a)f(x)|,若
正确答案
解:(1)函数

当 a+



于是﹣3≤﹣1+
即f(x)值域为[﹣3,﹣2].
(2)∵f(2a﹣x)+f(x)=

对定义域内的所有x都成立,
∴对定义域内的任意x,f(2a﹣x)+f(x)的值是定值﹣2.
(3)解:当a=1时,g(x)=x2+|x|(x≠﹣1)
(ⅰ)当x≥0时,
则函数g(x)在[0,+∞)上单调递增,
g(x)min=g(0)=0
(ⅱ)当x≤0时,
则函数g(x)在(﹣∞,0]且x≠﹣1时单调递减,
g(x)min=g(0)=0
综合得:当x≠﹣1时,g(x)的最小值是0.
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数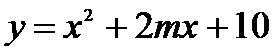
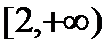
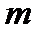
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.如图所示,过抛物线





正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在直三棱柱




(Ⅰ)求证:

(Ⅱ)求二面角
(Ⅲ)试问线段





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若直线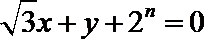
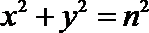
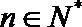
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.(1)直线经过点P(3,2),且在两坐标轴上的截距相等,求直线方程;
(2)设直线


正确答案
(1)设直线l在x,y轴上的截距均为a,
若a=0,即l过点(0,0)和(3,2),
∴l的方程为y=
若a≠0,则设l的方程为
∵l过点(3,2),∴
∴a=5,∴l的方程为x+y-5=0,
综上可知,直线l的方程为2x-3y=0或x+y-5=0.
(2)圆心(1,2),半径r=2
设圆心到直线的距离为d,则由垂径定理知


解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列








(2)若


正确答案
(1)由
相减得:

∵当

∴数列
(2)∵
由题意
设

∴


故
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析