- 导数的加法与减法法则
- 共610题
12.等边三角形





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数

(1)若


(2)设





正确答案
(1)
由
解得
(2)

当


因此当
解析
解析已在路上飞奔,马上就到!
知识点
14.如图,已知抛物线























正确答案
2/3
解析
解析已在路上飞奔,马上就到!
知识点
11.过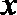
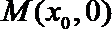
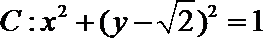
若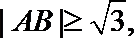
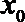
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.矩阵变换式



正确答案
1,6
解析
解析已在路上飞奔,马上就到!
知识点
11.一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰快,容器内盛有


(1)任意摆放该容器,当水面静止时,水面都恰好经过点
(2)正四棱锥的高等于正四棱柱的高的一半;
(3)若往容器内再注
(4)将容器侧面水平放置时,水面也恰好过
其中真命题的代号为____________。
正确答案
(3)(4)
解析
解析已在路上飞奔,马上就到!
知识点
16.某商场在国庆黄金周的促销活动中,对10月2号9时至14时的销售额进行统计,其频率分布直方图如图1所示.已知9时至10时的销售额为2.5万元,则11时至12时的销售额为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.对于数列












(1)试问


(2)设




(ⅰ)求

(ⅱ)若数列



正确答案
(1)数列





以下重复出现,所以不会出现所有项均为
(2)(ⅰ)因为




所以


当
由



当


(ⅱ)方法一:由









由此可见,经过


“结构”完全相同,但最大项减少12.
因为




接下来经过“







从以上分析可知,以后重复出现,所以数列各项和不会更小.
所以经过



方法二:若一个数列有三项,且最小项为


若数列



所以与





因此,数列



通过列举,不难发现各项为

所以,至少通过



解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析