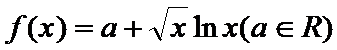- 导数的加法与减法法则
- 共610题
21.设函数f(x)=c lnx+
(Ⅰ)若x=1为f(x)的极大值点,求f(x)的单调区间(用c表示);
(Ⅱ)若f(x)=0恰有两解,求实数c的取值范围.
正确答案
(1)见解析;(2)
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:

∵x=1为f(x)的极值点,∴f'(1)=0,
∴
(I)若x=1为f(x)的极大值点,
∴c>1,当0<x<1时,f'(x)>0;当1<x<c时,f'(x)<0;
当x>c时,f'(x)>0.∴f(x)的递增区间为(0,1),(c,+∞);递减区间为(1,c).
(II)①若c<0,则f(x)在(0,1)上递减,在(1,+∞)上递增,
f(x)=0恰有两解,则f(1)<0,即

②若0<c<1,则f(x)的极大值为f(c)=clnc+
f
则

f
③若c>1,则


综上,使f(x)=0恰有两解的c的范围为: 
考查方向
解题思路
(1)先由1为极值点求出b+c+1=0,再有导数范围求单调区间;
(2)更具参数c的范围进行讨论.
易错点
第二问对题中所给条件不知如何下手导致失分。
知识点
12.已知a > 0,若函数
零点,则a的取值范围是( )
正确答案
解析
函数g(x)= f(x)+2a零点的个数等价于方程f(x)=-2a根的个数等价于函数 y=f(x)的图象与直线y=-2a交点的个数。本题直接计算比较麻烦,可采用特殊值验证即可,当a=1时,y=f(x)的图象如图(1),满足;当a=2时,y=f(x)的图象如图(2),也满足。故选(D)
考查方向
解题思路
思路一:先讨论函数f(x)在每一段内的单调性和取值范围,再根据g(x)= f(x)+2a至少有三个零点,转化为方程f(x)= -2a至少有三个实数根,再转化为函数 y=f(x)的图象与直线y=-2a至少有三个交点。思路二:由于本题是选择题,可以采用特殊值检验即可。
易错点
1、本题易在求分段函数的取值范围时发生错误。2、本题不容易画出函数y= f(x)的大致图像,不会把函数的零点转化为方程根的个数,更不会转化为两个图象交点个数问题,导致题目无法进行。
知识点
21.已知函数f(x)=ex+ax+b(a,b∈R,e是自然对数的底数)在点(0,1)处的切线与x轴平行. (Ⅰ)求a,b的值; (Ⅱ)若对一切x∈R,关于x的不等式f(x)≥(m-1)x+n恒成立,求m+n的最大值.
正确答案




解析
求导得

解得
所以不等式
令
当


当


当


即当



故当

即
令


当



故当



即

方法二:由(Ⅰ)知
所以不等式
即函数


要使



则有

所以
以下解法同上
考查方向
解题思路
解题步骤如下:先将点(0,1)代入函数解析式,然后求导代值即可建立关于a,b的方程组。构造函数
易错点
1、本题易在讨论m得取值范围时发生错误 。2、本题不容易构造函数,讨论其单调性,求其最值,导致题目无法进行。
知识点
13. 函数
正确答案
(3,0)
解析
当x=3时,无论a的值是多少,其对数值都为0,所以答案为(3,0).
考查方向
解题思路
知道对数的真数为1即可。
易错点
本题不知道1的对数值恒为0。
知识点
函数

26.当a=1时,求函数
27.①若存在实数


②若有且只有唯一整数


正确答案



解析
试题分析:本题属于函数与导数的问题,(1)考查求函数的单调区间,(2)1.参数的取值范围,2.参数的取值范围。
当a=1时,

由于
当


当


所以


考查方向
解题思路
(1)利用导数与函数的单调性的关系来求,
(2)1.构造函数求解,
2.利用导数求解。
易错点
分类讨论的思想讨论不完全。
正确答案
1.a的取值范围为
2.a的取值范围为
解析
试题分析:本题属于函数与导数的问题,(1)考查求函数的单调区间,(2)1.参数的取值范围,2.参数的取值范围。
①由

当
当



记


∴ 




∴ 当



综上所述,所有a的取值范围为
②由①知



又



∴


当



又



∴

综上所述,所有a的取值范围为
考查方向
解题思路
(1)利用导数与函数的单调性的关系来求,
(2)1.构造函数求解,2.利用导数求解。
易错点
分类讨论的思想讨论不完全。
4.设函数

正确答案
解析
由-2<0知知
考查方向
解题思路
根据自变量的取值范围,代入相应的解析式即可求值。
易错点
忽略分段函数的定义域导致出错。
知识点
14.已知函数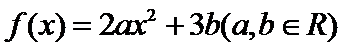
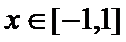
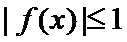
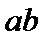
正确答案
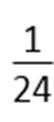
解析
由|f(x)|≤1,得|2a+3b|≤1,
所以,6ab≤|2a·3b|=|2a+3b-3b|·|3b|≤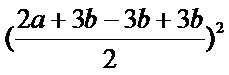
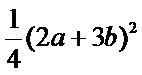
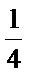
且当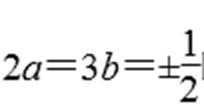
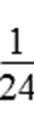
考查方向
解题思路
本题主要考查二次函数.函数性质.基本不等式.绝对值的概念.解题步骤如下:
由任意性,想到用端点值代入,得到不等式|2a+3b|≤1。
配凑出能使用基本不等式的式子。
易错点
本题不易想到使用基本不等式的配凑法,不能正确理解条件中的“任意”二字。
知识点
19.已知函数
(1)求函数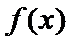
(2)试求函数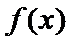
正确答案
(1)函数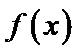
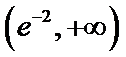
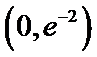
(2)当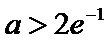
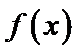
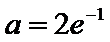
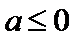
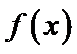
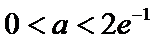
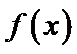
解析
试题分析:此题属于导数的常规问题,难度较大。函数的单调性,最值,零点的个数等等,都可利用导数加以解决。
(1)由函数f(x)=a+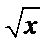
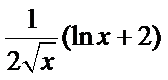
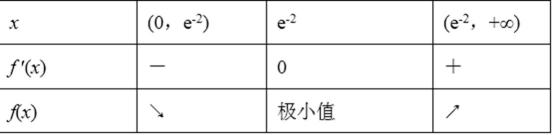
令f ′(x)=0,得 x=e-2.列表如下:
因此,函数f(x)
(2)由(1)可知,fmin(x)=f(e-2)=a-2e-1.
(i)当a>2e-1时,由f(x)≥f(e-2)=a-2e-1>0,得函数f(x)的零点个数为0.
(ii)当a=2e-1时,因f(x)在(e-2,+∞)上是单调增,在(0,e-2)上单调减,
故x∈(0,e-2)∪(e-2,+∞)时,f(x)>f(e-2)=0.
此时,函数f(x)的零点个数为1.
(iii)当a<2e-1时,fmin(x)=f(e-2)=a-2e-1<0.
①a≤0时,
因为当x∈(0,e-2]时,f(x)=a+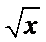
所以,函数f(x)在区间(0,e-2]上无零点;
另一方面,因为f(x)在[e-2,+∞)单调递增,且f(e-2)=a-2e-1<0,
又e-2a∈(e-2,+∞),且f(e-2a)=a(1-2e-a)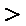
此时,函数f(x)在(e-2,+∞)上有且只有一个零点.
所以,当a≤0时,函数f(x)零点个数为1.
②0<a<2e-1时,
因为f(x)在[e-2,+∞)上单调递增,且f(1)=a>0,f(e-2)=a-2e-1<0,
所以,函数f(x)在区间(e-2,+∞)有且只有1个零点;
另一方面,因为f(x)在(0,e-2]上是单调递减,且f(e-2)=a-2e-1<0
又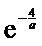
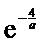
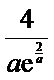
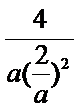
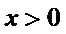
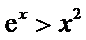
此时,函数f(x)在(0,e-2)上有且只有1个零点.
所以,当0<a<2e-1时,函数f(x)零点个数为2.
综上所述,当a>2e-1时,f(x)的零点个数为0;当a=2e-1,或a≤0时,f(x)的零点个数为1;
当0<a<2e-1时,f(x)的零点个数为2.
考查方向
解题思路
本题主要考查函数的基本性质.导数的应用等基础知识。解题步骤如下:
求出导数,考察导数在指定区间上的正负号,从而得出函数的单调性;
把考察零点个数问题转化为函数的最值问题来解决。
易错点
第一问不能正确判断导函数在指定区间的正负号;
第二问不能理解考察零点的个数,可以转化为最值问题来处理。
知识点
16. 
正确答案
(3,3.5)
解析
由


考查方向
解题思路
对函数求导,根据导函数为3这个方程有2个大于0的根即可解出a的取值范围。
易错点
本题不知道转化为根的分布问题。
知识点
12. 定义在R上的函数





正确答案
解析
由











由图像可知该函数在一个周期内有2个零点,故函数


考查方向
解题思路
先利用


易错点
无法求出函数的周期导致出错。
知识点
扫码查看完整答案与解析