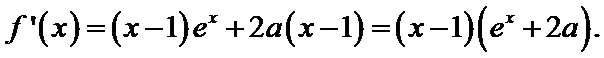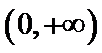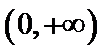导数的加法与减法法则
共610题

· 导数的加法与减法法则

导数的加法与减法法则
共610题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

10.已知函数为的导函数，则的值为__________.

正确答案

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

8.若a>b>0，0<c<1，则（）

Alogac<logbc

Blogca<logcb

Cac<bc

Dca>cb

正确答案

知识点

导数的加法与减法法则

题型：填空题

填空题 · 4 分

6．已知点（3,9）在函数的图像上，则的反函数=______.

正确答案

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

已知函数．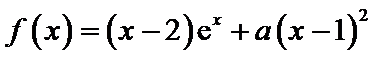

26.讨论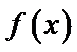的单调性；

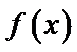
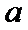
27.若有两个零点,求的取值范围.

第(1)小题正确答案及相关解析

正确答案

见解析

解析

(I)

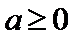
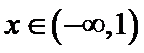
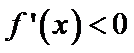
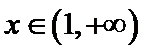
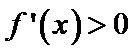
(i)设,则当时,；当时,.

所以在单调递减,在单调递增.

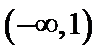
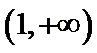
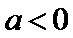
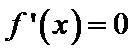
(ii)设,由得x=1或x=ln(-2a).

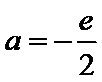
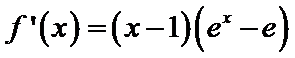
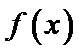
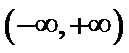
①若,则,所以在单调递增.

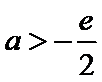
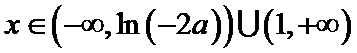
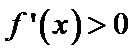
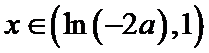
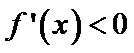
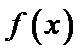
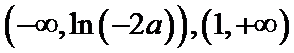
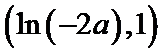
②若,则ln(-2a)<1,故当时,；

当时,,所以在单调递增,在单调递减.

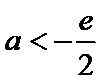
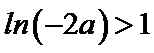
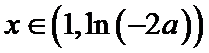
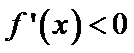
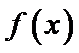
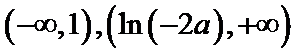
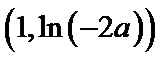
③若,则,故当时,,当时,,所以在单调递增,在单调递减.

考查方向

函数单调性,导数应用

解题思路

(I)先求得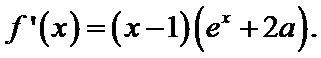再根据1,0,2a的大小进行分类确定的单调性；

易错点

分类讨论思想及分类讨论原则、合理构造新函数.

第(2)小题正确答案及相关解析

正确答案

解析

考查方向

函数单调性,导数应用

解题思路

(II)借助第一问的结论,通过分类讨论函数单调性,确定零点个数,从而可得a的取值范围为

易错点

分类讨论思想及分类讨论原则、合理构造新函数.

题型：填空题

填空题 · 4 分

6．已知点（3,9）在函数的图像上，则的反函数=______.

正确答案

解析

过点（3,9），所以，根据，得，所以，即=.

考查方向

反函数

解题思路

利用反函数的定义求解

易错点

反函数的定义

知识点

导数的加法与减法法则

题型：简答题

简答题 · 18 分

本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分

已知R，函数=.

28.当时，解不等式>1；

29.若关于的方程+=0的解集中恰有一个元素，求的值；

30.设>0，若对任意，函数在区间上的最大值与最小值的差不超过1，求的取值范围.

第(1)小题正确答案及相关解析

正确答案

解析

由，得，

解得．

考查方向

解不等式

解题思路

一般的解不等式

易错点

分类讨论，转化思想,

第(2)小题正确答案及相关解析

正确答案

或

解析

有且仅有一解，

等价于有且仅有一解，等价于有且仅有一解．

当时，，符合题意；

当时，，．

综上，或．

考查方向

函数与方程

解题思路

直接求方程的跟

易错点

分类讨论，转化思想,

第(3)小题正确答案及相关解析

正确答案

的取值范围为．

解析

当时，，，

所以在上单调递减．

函数在区间上的最大值与最小值分别为，．

即，对任意

成立．

因为，所以函数在区间上单调递增，时，

有最小值，由，得．

故的取值范围为．

考查方向

函数性质的综合应用；

解题思路

根据单调性求最值.

易错点

分类讨论，转化思想,

题型：填空题

填空题 · 5 分

13．如图，及其内部的点组成的集合记为，为中任意一点，则的最大值为．

正确答案

解析

由题图可知，目标函数，因此当，即在点处时取得最大值为.

考查方向

本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．

解题思路

本题主要考查的是线性规划，属于容易题．线性规划类问题的解题关键是先正确画出不等式组所表示的平面区域，然后确定目标函数的几何意义，通过数形结合确定目标函数何时取得最值．

易错点

要看清楚是求“最大值”还是求“最小值”，否则很容易出现错误．

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

10．若定义在上的函数满足，其导函数满足，则下列结论中一定错误的是（）

正确答案

解析

由已知条件，构造函数，则，故函数在上单调递增，且，故，所以，，所以结论中一定错误的是C，选项D无法判断；构造函数，则，所以函数在上单调递增，且，所以，即，，选项A,B无法判断，故选C．

考查方向

函数与导数．

解题思路

根据导数的概念求出K的取值范围，然后代入不等式中，可以判断出答案。

易错点

函数和导数的综合性质掌握不全面，不理解导数的定义式，不会构造函数

知识点

导数的加法与减法法则

题型：简答题

简答题 · 14 分

20.设函数，，其中

（Ⅰ）求的单调区间；

（Ⅱ）若存在极值点，且，其中，求证：；

（Ⅲ）设，函数，求证：在区间上的最大值不小于.

正确答案

（Ⅰ）递减区间为，递增区间为，.（Ⅱ）详见解析（Ⅲ）详见解析

解析

试题分析：（Ⅰ）先求函数的导数：，再根据导函数零点是否存在情况，分类讨论：①当时，有恒成立，所以的单调增区间为.②当时，存在三个单调区间（Ⅱ）由题意得即，再由化简可得结论（Ⅲ）实质研究函数最大值：主要比较，的大小即可，分三种情况研究①当时，，②当时，，③当时，.

试题解析：（1）解：由，可得，下面分两种情况讨论：

①当时，有恒成立，所以的单调增区间为.

②当时，令，解得或.

当变化时，、的变化情况如下表：

所以的单调递减区间为，单调递增区间为，.

（2）证明：因为存在极值点，所以由（1）知且.

由题意得，即，

进而，

又，且，

由题意及（1）知，存在唯一实数满足，学科&网且，因此，

所以.

（3）证明：设在区间上的最大值为，表示，两数的最大值，下面分三种情况讨论：

①当时，，由（1）知在区间上单调递减，

所以在区间上的取值范围为，因此，

所以.

②当时，，

由（1）和（2）知，，

所以在区间上的取值范围为，

所以

③当时，，由（1）和（2）知，

，，

所以在区间上的取值范围为，因此，

综上所述，当时，在区间上的最大值不小于.

考查方向

导数的运算，利用导数研究函数的性质、证明不等式

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

16.已知f(x)为偶函数，当时，，则曲线y= f(x)在点(1,2)处的切线方程式是_____________________________.

正确答案

知识点

导数的加法与减法法则

继续学习学习下一知识点

下一知识点 : 导数的乘法与除法法则

百度题库 > 高考 > 文科数学 > 导数的加法与减法法则

扫码查看完整答案与解析