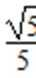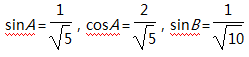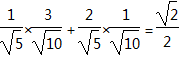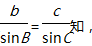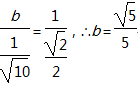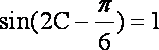余弦定理
共104题

· 余弦定理

余弦定理
共104题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

△ABC中，角A、B、C的对边分别为，S是△ABC的面积，且，则_________。

正确答案

-1

解析

略

知识点

诱导公式的作用正弦定理余弦定理

题型：简答题

简答题 · 13 分

在△ABC中，角A、B、C的所对应边分别为a,b,c，且

（1）求c的值；

（2）求的值。

正确答案

见解析

解析

（1）根据正弦定理，,所以-------------5分

（2）根据余弦定理，得

于是

从而

………12分

所以-------------------13分

知识点

正弦定理余弦定理

题型：简答题

简答题 · 14 分

已知分别为△三个内角、、所对的边长，且。

（1）求：的值；

（2）若，，求、。

正确答案

（1）4（2）,2

解析

解析：（1）由正弦定理得，2分

又，所以， 5分

可得。··················································································· 7分

（2）若，则，，，得，可得，。···································································································································· 10分

，

由正弦定理得

，························································ 14分

知识点

正弦定理余弦定理

题型：简答题

简答题 · 14 分

在中，角，，所对的边长分别为，，，向量，，且。

（1）求角；

（2）若，，成等差数列，且，求的面积。

正确答案

（1）（2）

解析

解析：（1），，，，……………………5分

又，，，………………7分

（2），，。

又，，即……10分

将代入得，得，从而，三角形为等边三角形，……12分

，………………14分

知识点

余弦定理

题型：简答题

简答题 · 12 分

在ABC中，内角A，B，C的对边分别为.已知=2，若cosB=且的周长为5，求边的长。

正确答案

见解析。

解析

因为=2,所以有,即,

又因为的周长为5,所以,

由余弦定理得：

，

即，

解得=1，所以=2.

知识点

正弦定理余弦定理

题型：简答题

简答题 · 8 分

在中，分别为内角的对边，且

（1）求的大小；

（2）若，试求内角B、C的大小。

正确答案

见解析。

解析

（1）∵

由余弦定理得

故 -----------------4分

（2）∵，

∴， ----------------5分

∴，

∴ ----------------6分

又∵为三角形内角， ----------------7分

故. -----------------8分

知识点

正弦定理余弦定理

题型：简答题

简答题 · 12 分

在中,分别为的对角,且是等差中项。

（1）求的值。

（2）若的面积为,为边的中点,求中线的最小值。

正确答案

见解析。

解析

（1）是等差中项

由正弦定理得:

故

在中,

故

所以

（2）由题意知

故

由向量知识得

故

即

所以的最小值为。

知识点

余弦定理

题型：填空题

填空题 · 5 分

在△ABC中，，若最长边为1，则最短边的长为。

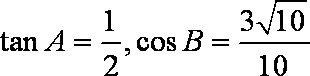
正确答案

解析

由tanA>0，cosB>0知A、B均为锐角，

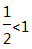
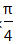
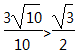
∵tanA＝，∴0<A<，cosB＝， ∴0<B<，∴C为最大角，

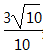
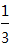
由cosB＝知，tanB＝，∴B<A，∴b为最短边，

由条件知，，

∴sinC＝sin（A＋B）＝sinAcosB＋cosAsinB＝

，

由正弦定理

知识点

同角三角函数间的基本关系两角和与差的正切函数余弦定理

题型：简答题

简答题 · 12 分

已知函数.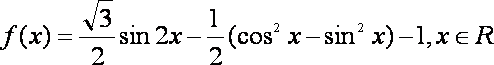

（1）求函数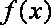的单调递增区间；

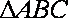
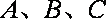
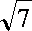
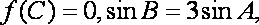
（2）设的内角的对边分别为a、b、c，若c=，求a,b的值

正确答案

见解析。

解析

（1）………………………………4分

……………………………6分

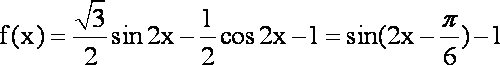
（2）由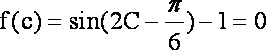得

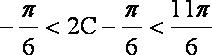
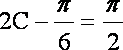
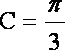
又，所以，即……………………………………8分

由余弦定理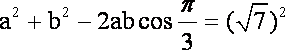①…………………………………………………10分

由得②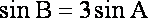

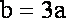
由①②得，a=1,b=3………………………………………………………………………12分

知识点

正弦函数的单调性三角函数中的恒等变换应用正弦定理余弦定理

题型：简答题

简答题 · 10 分

锐角三角形ABC的三内角A、B、C所对边的长分别为，设向量，且

（1）求角B的大小；

（2）若，求的取值范围。

正确答案

见解析。

解析

（1）

，

即

（2）

三角形ABC为锐角三角形，

，且

知识点

余弦定理平面向量共线（平行）的坐标表示

继续学习学习下一知识点

下一知识点 : 余弦定理的应用

百度题库 > 高考 > 文科数学 > 余弦定理

扫码查看完整答案与解析