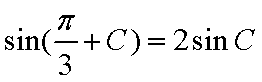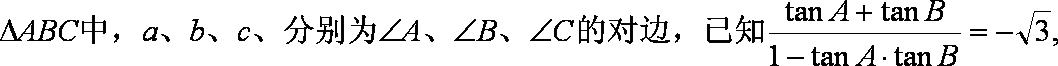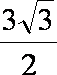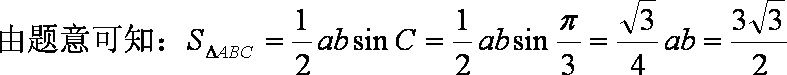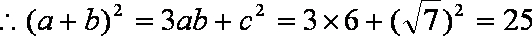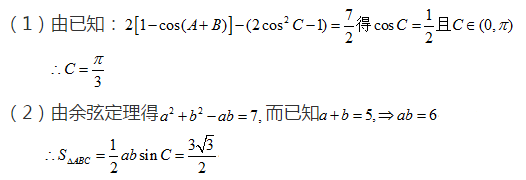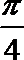- 余弦定理
- 共104题




若




(1)求A,B,C;
(2)若函数



正确答案
见解析。
解析
(1)根据题意得


∴


(2)∵



又∵



由
知识点
在
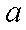
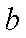

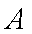
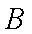
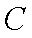

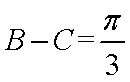
(1) 求角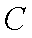
(2) 若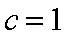
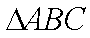
正确答案
见解析
解析
(1)由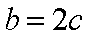
又由正弦定理,得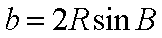
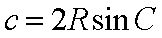
将其代入上式,得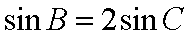
∵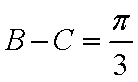
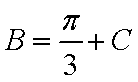
∴
整理得,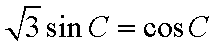
∴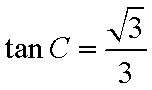
∵角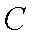
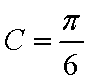
(2) ∵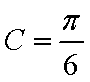
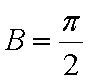
又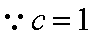
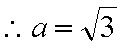
∴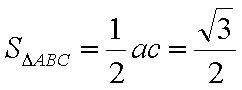
知识点
在

(1)求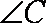
(2)求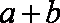
正确答案
见解析。
解析
(1)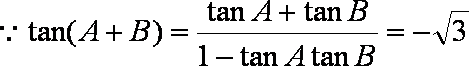
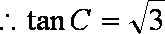

又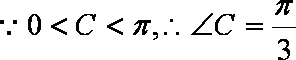
(2)
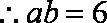
由余弦定理可得: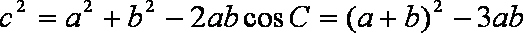
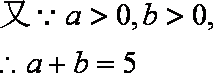
知识点
在


(1)求角C
(2)求
正确答案
见解析
解析
解析:
(1)

所以


(2)
因为





故

知识点
已知函数
(1)当

(2)设△ABC的内角A,B,C的对应边分别为a,b,c,且


正确答案
见解析
解析
(1)

令
解得



(2)由
而


因为向量


由正弦定理得:
由余弦定理得:
由①②解得
知识点
16. 在△

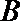
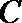
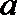
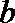
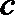
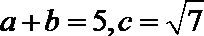
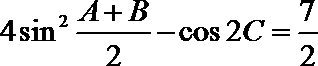
(Ⅰ)求角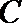
(Ⅱ)求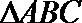
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.在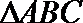



(1)求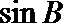
(2)若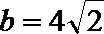
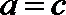
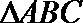
正确答案
(1)由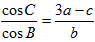

即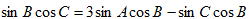
∴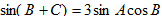

∵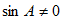
∴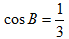
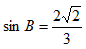
(2)∵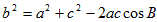
32=
∵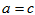
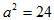
解析
解析已在路上飞奔,马上就到!
知识点
5.


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. △ABC中,角A、B、C的对边分别为a,b,c,若S表示△ABC的面积,若acosB+bcosA=csinC,,且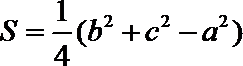
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 在



(1)求角
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析