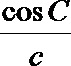余弦定理
共104题

· 余弦定理

余弦定理
共104题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

12．在ABC中，a，b，c分别是角A，B，C的对边．已知a，b，c成等比数列，且＝ac－bc，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理等比数列的性质及应用

题型：简答题

简答题 · 12 分

17．已知函数

（I）求函数的最小值和最小值时x的集合；

（II）设△ABC的内角A，B，C对边分别为a，b，c，且与的值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用正弦定理余弦定理三角函数的最值平行向量与共线向量

题型：单选题

单选题 · 5 分

5．在△ABC中，sin2A≤sin2B＋sin2C－sinBsinC，则A的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理

题型：单选题

单选题 · 5 分

3．在△ABC中，，且△ABC的面积为，则BC的长为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理

题型：简答题

简答题 · 12 分

16．向量，已知a∥b，且有函数．

（1）求函数的最小正周期;

（2）已知锐角△ABCC的三个内角分别为A,B,C，若有，边，求AC的长及△ABC的面积．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用正弦定理余弦定理平面向量共线（平行）的坐标表示

题型：简答题

简答题 · 12 分

17．在中，内角的对边分别为，且。

（1）求角的大小；

（2）若，求的面积。

正确答案

（1）由及余弦定理或正弦定理可得

所以

（2）由余弦定理a2＝b2＋c2－2bccos A，得b2＋c2－bc＝36．又b＋c＝8，所以bc＝．

由三角形面积公式S＝bcsin A，得△ABC的面积为．

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理

题型：简答题

简答题 · 14 分

17．如图，某测量人员为了测量珠江北岸不能到达的两点A，B之间的距离，他在珠江南岸找到一个点C，从C点可以观察到点A，B；找到一个点D，从D点可以观察到点A，C；找到一个点E，从E点可以观察到点B，C；并测量得到数据：∠ACD＝90°，∠ADC＝60°，∠ACB＝15°，∠BCE＝105°，∠CEB＝45°，CD＝CE＝100m．

（1）求△CDE的面积；

（2）求A，B之间的距离．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

余弦定理解三角形的实际应用

题型：简答题

简答题 · 13 分

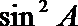
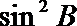
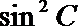
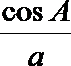
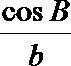
19．在不等边△ABC中，设A．B．C所对的边分别为a，b，c，已知，，依次成等差数列，给定数列，，

（1）试根据下列选项作出判断，并在括号内填上你认为是正确选项的代号（　）

A．是等比数列而不是等差数列　

B．是等差数列而不是等比数列

C．既是等比数列也是等差数列　

D．既非等比数列也非等差数列

（2）证明你的判断

正确答案

（1）B

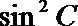
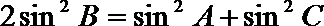
（2）因为、、成等差数列，所以，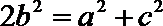

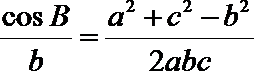
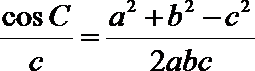
所以．又，，．

显然，即、、成等差数列．若其为等比数列，有，所以，，与题设矛盾

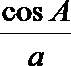
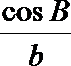
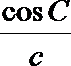
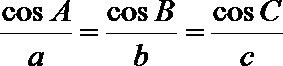
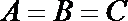
解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理等差数列的判断与证明等比数列的判断与证明

题型：简答题

简答题 · 12 分

17．在△ABC中，内角A，B，C的对边分别为a，b，c，已知a，b，c成等比数列，且．

（1）若求a＋c的值；

（2）求的值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理平面向量数量积的运算向量在几何中的应用

题型：简答题

简答题 · 12 分

16．向量，已知a∥b，且有函数．

（1）求函数的最小正周期;

（2）已知锐角△ABCC的三个内角分别为A,B,C，若有，边，求AC的长及△ABC的面积．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两角和与差的正弦函数正弦定理余弦定理平行向量与共线向量

继续学习学习下一知识点

下一知识点 : 余弦定理的应用

百度题库 > 高考 > 文科数学 > 余弦定理

扫码查看完整答案与解析