- 余弦定理
- 共104题
10.如图,正方形







正确答案
解析



知识点
18.



(Ⅰ)求角
(Ⅱ)若




正确答案
(Ⅰ)在

而

(Ⅱ)由

同理
∴
∵

∴


解析
解析已在路上飞奔,马上就到!
知识点
9.在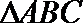
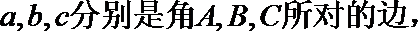
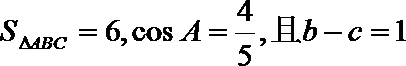

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量
(1)求
(2)在









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 在








(Ⅰ)求角
(Ⅱ)设

正确答案
(Ⅰ)


∴

(Ⅱ)由
知
∴

由正弦定理得:
解析
解析已在路上飞奔,马上就到!
知识点
13.在


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
9.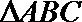



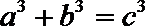
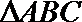
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数
(Ⅰ)求函数
(Ⅱ)记



正确答案
(Ⅰ)
所以函数

(Ⅱ)由

又因为
所以

因为
所以由正弦定理
故
当
当
故
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析


































