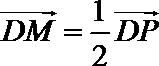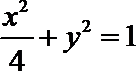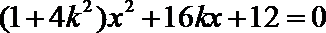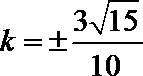- 相关点法求轨迹方程
- 共16题
已知抛物线








23.若




24.若


正确答案
(Ⅰ)由题设









设AR的斜率为

所以
解析
由题设









设AR的斜率为

所以
考查方向
解题思路
(I)设出与x轴垂直的两条直线,然后得出A,B,P,Q,R的坐标,然后通过证明直线AR与直线FQ的斜率相等即可证明结果了;
易错点
对抛物线定义与几何性质、直线与抛物线位置关系和轨迹求法理解出现错误、计算错误
正确答案
(Ⅱ)
解析
(Ⅱ)设


则
由题设可得


设满足条件的

当



而

当



考查方向
解题思路
(II)设直线l与x轴的交点坐标


易错点
对抛物线定义与几何性质、直线与抛物线位置关系和轨迹求法理解出现错误、计算错误
9.已知圆C:x2+y2=16,过点P(2,3)作直线l交圆C于A,B两点,分别过A,B两点作圆C的切线,若两条切线相交于点Q,则点Q的轨迹方程为_______.
正确答案
2x+3y=16
解析
设A(x1,y1),B(x2,y2),Q(m,n),则直线AQ的方程为x1x+y1y=16,直线BQ的方程为x2x+y2y=16,
因为点Q为两直线的交点,所以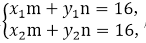
知识点
已知







正确答案
解析
第一步识别条件:椭圆





第二步转化条件: 应该想到在向量一章里面学过这个重心的坐标表示可以用三个顶点表示啊 G((x1+x2+x3)/3,(y1+y2+y3)/3),再看看图形,发现太好了, 三个点中,F1,F2关于原点是对称的,x1+x2=0,y1+y2=0这下可好了。
第三步看问定向:重心
第四步结论已出现:
知识点
20.已知圆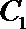
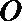
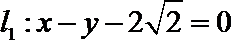
(1)求圆的标准方程;
(2)设点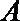
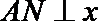

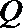
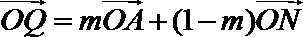
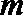
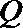

(3)在(2)的结论下,当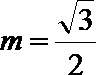
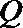
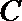
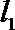
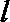

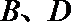
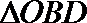
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
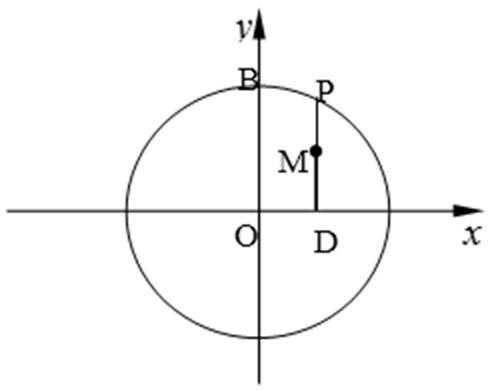
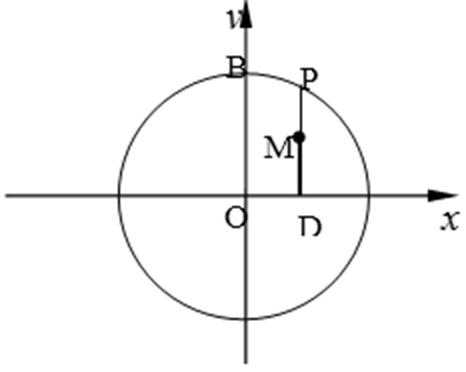
21.如图,圆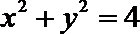
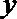
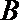
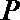

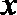
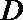
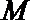
(1)求动点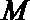
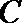
(2)过点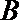
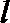

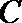
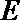
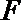

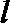
正确答案
(1)设
则由题意得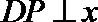
所以
又P在圆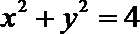
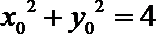
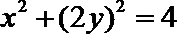
轨迹是以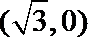
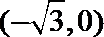
长轴长为4的椭圆。
(2)方法一:当直线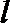
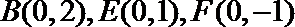
设直线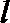
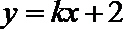
代入椭圆方程得:
△
设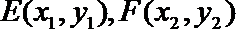
则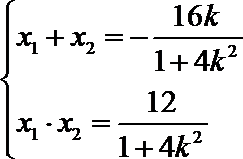
由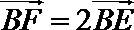
所以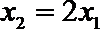
由(*)、(**)
解得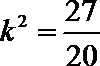
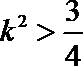
所以
即所求直线方程为: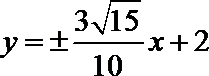
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析