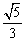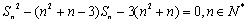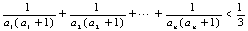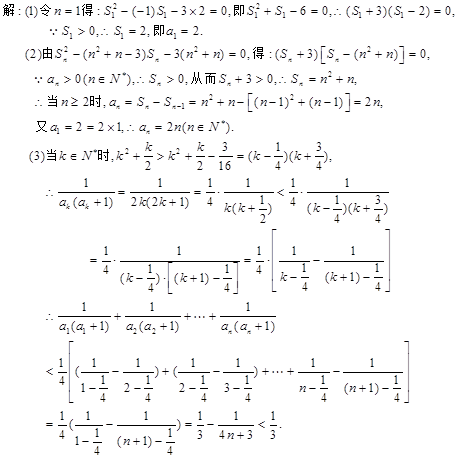- 由递推关系式求数列的通项公式
- 共97题
已知椭圆
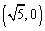
(1)求椭圆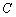
(2)若动点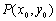
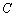
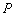
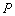
正确答案
见解析。
解析
知识点
设

正确答案
解析
=
=
≥2+2=4
当且仅当ab=1,a(a-b)=1时等号成立
如取a=

知识点
已知{an}是等差数列,其前n项和为Sn,{bn}是等比数列,且a1=b1=2,a4+b4=27,S4-b4=10。
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=a1b1+a2b2+…+anbn,n∈N*,证明Tn-8=an-1bn+1(n∈N*,n>2)。
正确答案
(1) an=3n-1,bn=2n,n∈N*,;(2)略
解析
(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,由a1=b1=2,得a4=2+3d,b4=2q3,S4=8+6d。
由条件,得方程组
所以an=3n-1,bn=2n,n∈N*。
(2证明:由(1)得
Tn=2×2+5×22+8×23+…+(3n-1)×2n,①
2Tn=2×22+5×23+…+(3n-4)×2n+(3n-1)×2n+1。②
由①-②,得
-Tn=2×2+3×22+3×23+…+3×2n-(3n-1)×2n+1
=
即Tn-8=(3n-4)×2n+1,
而当n>2时,an-1bn+1=(3n-4)×2n+1。
所以,Tn-8=an-1bn+1,n∈N*,n>2
知识点
设各项为正数的数列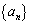
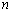

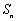
(1)求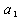
(2)求数列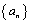
(3)证明:对一切正整数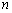
正确答案
见解析。
解析
知识点
数列{an}满足an+1=
正确答案
解析
解析:由题意得,an+1=


令n=6代入得,a7=

根据以上结果发现,求得结果按2,
知识点
扫码查看完整答案与解析