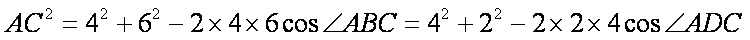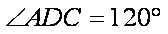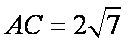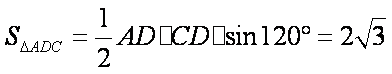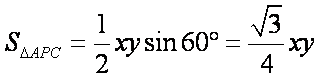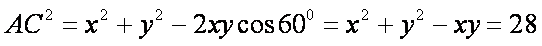- 构成空间几何体的基本元素
- 共31题
某几何体的三视图如图所示(单位:cm),则该几何体的表面积是cm2,体积是

正确答案
72;32
知识点
10.补写出下列句子中的空缺部分。
(1)孟子在《生于忧患,死于安乐》中论证人有过错而后改时,用“ ,
。”两句表述了人们发现错误、改正错误的过程。
(2)《诗经·氓》一诗中,“ , 。”沉痛地写出了女子没有什么过错,而男子的行为却前后不一致的情形。
(3)在《庄子·逍遥游》中,先说“覆杯水于坳堂”能使当作船的“芥”浮起来,又从反面说明水深才能承载大船的道理的两句是“ , ”。
正确答案
(1)困于心衡于虑而后作 征于色发于声而后喻
(2)女也不爽 士贰其行
(3)(且夫)水之积也不厚 则其负大舟也无力(“且夫”有无皆可)
解析
第一题的关键“人们发现错误、改正错误”;第二题的关键是“女子没有什么过错,而男子的行为却前后不一致”;第三题从“先说”可知,所填内容应在“覆杯水于坳堂”这句之后,再根据“从反面说明水深才能承载大船的道理”即可得出答案。
考查方向
解题思路
回忆要求默写的文章,根据提示寻找答案。
易错点
第二题考生容易填成“士也罔极,二三其德”。
知识点
12.给出如下四个命题:
①

②

③函数




④ 若函数



其中正确的命题是( )(写出所有正确命题的题号)。
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
已知函数
(1)当


(2)讨论函数
(3)若


正确答案
(1)
(2)当









(3)
解析
(1)


当


曲线



(2)
(a)当



------------------1分
(b)当

由


由


所以函数


------------------3分
(c)当

由


由


所以函数


------------------5分
(3)由(2)知,当



递增,所以函数


则有

当




又
(或者说明





所以当

知识点
已知函数





(1)求

(2)若不等式


(3)若

正确答案
见解析
解析
(1)
因为




(2)由已知可得
所以

化为




记


所以

(3)原方程可化为
令








记

或
解不等组①,得


………………(2分)
知识点
样本中共有五个个体,其值分别为
正确答案
解析
∵由题可知样本的平均值为1,∴5(a+0+1+2+3)=1,解得a=-1,
∴样本的方差为5(1)[(-1-1)2+(0-1)2+(1-1)2+(2-1)2+(3-1)2]=2.
知识点
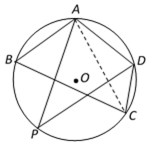
某市某棚户区改造建筑用地平面示意图如图所示,经规划调研确定,棚改规划建筑用地区域是半径为R的圆面,该圆面的内接四边形ABCD是原棚户

(1)请计算原棚户区建筑用地ABCD的面积及圆面的半径R的值;
(2)因地理条件的限制,边界AD、DC不能变更,而边界AB、BC可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧ABC上设计一点P,使得棚户区改造的新建筑用地APCD的面积最大,并求最大值。
正确答案
见解析
解析
(1)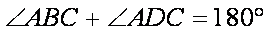
∴ 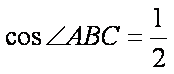
∵ 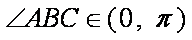
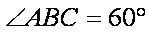
S四边形ABCD =
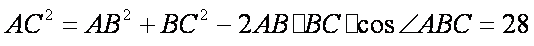
由正弦定理得:
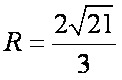
(2)S四边形APCD = 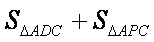
设AP = x,CP = y
由余弦定理得:
∴ 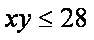
∴S四边
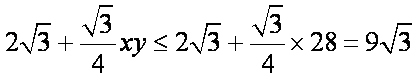
∴ 作AC的垂直平分线与圆弧ABC的交点即为点P,最大面积为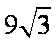
知识点
在正方体






正确答案
解析
略
知识点
某几何体的三视图如题(7)图所示,其侧视图是一个边长为l的等边三角形,俯视图是两个正三角形拼成
正确答案
解析
由几何体的三视图可知:此几何体是两个相同的三棱锥拼接而成的,由侧视图知三棱锥的高为


故选:C
知识点
如图,在多面体ABCDE中,





(1)求证:

(2)求多面体ABCDE的体积;
(3)求平面ECD和平面ACB所成的锐二面角的余弦值。
正确答案
见解析
解析
(1)找BC中点G点,连接AG,FG
∴F,G分别为DC,BC中点
∴FG
∴四边形EFGA为平行四边形
∴
∵AE
∴
又∵
∴平面ABC
又∵G为BC中点且AC=AB=BC
∴AG
∴AG
∴EF
(2)过作C作CH

∴
(3)以H为原点建立如图所示的空间直角坐标系
则
设平面CEF的法向量为
由

平面ABC的法向量为
则
∴平面角ECD和平面ACB所成的锐二面角的余弦值为
知识点
扫码查看完整答案与解析