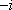• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
  • 棱柱的结构特征
  • 共46题
  • 棱柱的结构特征
  • 共46题

热门试卷

X 查看更多试卷
1
题型：填空题
|
填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1
题型：填空题
|
填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1
题型：填空题
|
填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1
题型：填空题
|
填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1
题型：简答题
|
简答题 · 13 分

如题（19）图，四棱锥中，底面是以为中心的菱形，底面，

，为上一点，且.

(1)求的长；

(2)求二面角的正弦值.

正确答案

（1）PO的长为。

（2）=

解析

（1）连接AC，BD，

∵底面是以O为中心的菱形，PO⊥底面ABCD，

故AC∩BD=O，且AC⊥BD，

以O为坐标原点，OA，OB，OP方向为x，y，z轴正方向建立空间坐标系O﹣xyz，

∵AB=2，∠BAD=，

∴OA=AB•cos（∠BAD）=，OB=AB•sin（∠BAD）=1，

∴O（0，0，0），A（，0，0），B（0，1，0），C（﹣，0，0），

=（0，1，0），=（﹣，﹣1，0），

又∵BM=，

∴=（﹣，﹣，0），

则=+=（﹣，，0），

设P（0，0，a），则=（﹣，0，a），=（，﹣，a），

∵MP⊥AP，

∴•=﹣a2=0，

解得a=，

即PO的长为。

（2）由（1）知=（﹣，0，），=（，﹣，），=（，0，），

设平面APM的法向量=（x，y，z），平面PMC的法向量为=（a，b，c），

由，得，

令x=1，则=（1，，2），

由，得，

令a=1，则=（1，﹣，﹣2），

∵平面APM的法向量和平面PMC的法向量夹角θ满足：

cosθ===﹣

故sinθ==

知识点

棱柱的结构特征
1
题型：填空题
|
填空题 · 4 分

函数的值域是           .

正确答案

解析

根据题目，因为，所以.

知识点

棱柱的结构特征
1
题型： 单选题
|
单选题 · 5 分

已知正四棱柱ABCD－A1B1C1D1中，AA1＝2AB，则CD与平面BDC1所成角的正弦值等于(　　)。

A

B

C

D

正确答案

A

解析

如图，连结AC交BD于点O，连结C1O，过C作CH⊥C1O于点H.

∵

CH⊥平面C1BD，

∴∠HDC为CD与平面BDC1所成的角。

设AA1＝2AB＝2，则，.

由等面积法，得C1O·CH＝OC·CC1，即，

∴.

∴sin∠HDC＝.故选A.

知识点

棱柱的结构特征
1
题型： 单选题
|
单选题 · 5 分

i是虚数单位，计算i＋i2＋i3＝

A－1

B1

C

D

正确答案

A

解析

由复数性质知：i2＝－1

故i＋i2＋i3＝i＋(－1)＋(－i)＝－1

知识点

棱柱的结构特征
1
题型：简答题
|
简答题 · 12 分

某种有奖销售的饮料，瓶盖内印有“奖励一瓶”或“谢谢购买”字样，购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖，中奖概率为.甲、乙、丙三位同学每人购买了一瓶该饮料。

（1）求甲中奖且乙、丙都没有中奖的概率；

（2）求中奖人数ξ的分布列及数学期望Eξ.

正确答案

见解析。

解析

知识点

棱柱的结构特征
1
题型：简答题
|
简答题 · 13 分

如图，在三棱柱中中，是正方形的中心，，，且。

（1）求异面直线与所成角的余弦值；

（2）求二面角的正弦值；

（3）设为棱的中点，点在平面内，且，求线段的长。

正确答案

见解析

解析

解法１。如图所示，建立空间直角坐标系，其中点为坐标原点，所在直线为轴，所在直线为轴。

由题意，，，，，，。

（1） ,.

所以.

（2） ,，

设平面的法向量为，则即

令，则，。。

设平面的法向量为，则即

令，则，。。

于是，所以。

所以二面角的正弦值为。

（3）由为棱的中点，得，设点，

则。

因为，则

即

解得故，向量，

所以线段的长。

解法2。（1）由于,故是异面直线与所成的角。

因为，是正方形的中心，，，

所以，

，

因此。

（2）连接，因为及是的中点，则，又，，所以

。

过点作于，连，于是，

所以为二面角的平面角。

在中，，

连，在中，，，

，从而。

所以二面角的正弦值为。

（3）因为，所以，取的中点，连接。

由于为棱的中点，所以，且。

又，故，

因为，所以，连接并延长交于点，

则，故。

由，得。

延长交于，可得，连接。

在中，，由直角三角形的射影定理，，

所以，。

连接，在中，。

知识点

棱柱的结构特征
继续学习 学习下一知识点
下一知识点 : 棱锥的结构特征
百度题库 > 高考 > 理科数学 > 棱柱的结构特征

扫码查看完整答案与解析

  • 上一题
  • 1/10
  • 下一题