- 等差数列与等比数列的综合
- 共63题
4.在函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.数列
(1)求证:数列
(2)求数列
(3)等差数列


正确答案
(1)
又
所以
数列
(2)
(3)
等差数列
设公差为
则
又

解析
解析已在路上飞奔,马上就到!
知识点
6.在正项等比数列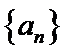
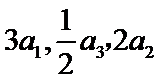
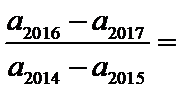
正确答案
解析
由题可知:a3=3a1+2a2,即a1q2=3a1+2a1q,解得q=-1(舍去)或q=2.a2016=a2014q2,
a2017=a2014q3,a2015=a2014q,约分即可。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
1、求出q;
2、代入计算,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在求q时发生错误。
知识点
设等比数列




18.求数列
19.设



正确答案
数列



解析
解:
即

考查方向
解题思路
利用数列的性质,建立方程,求出通项公式,在求和时进行分类。
易错点
求和时绝对值的分类讨论。
正确答案
数列



解析
解:



当
两式相减,得
考查方向
解题思路
利用数列的性质,建立方程,求出通项公式,在求和时进行分类。
易错点
求和时绝对值的分类讨论。
5. 已知数列


正确答案
解析
通过观察,可以看到,b2,b16和b9之间的关系,可以得到

考查方向
解题思路
利用等差中项求b9,进而求解答案
易错点
发现不到b2b16和b9之间的关系。
知识点
扫码查看完整答案与解析



































