- 一元二次不等式的解法
- 共209题
16.某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时.生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为 元.
正确答案
解析
试题分析:设生产产品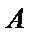
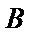
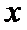
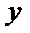
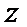
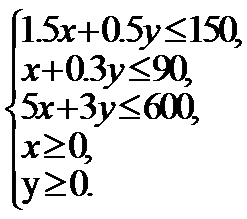
目标函数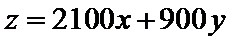
二元一次不等式组①等价于
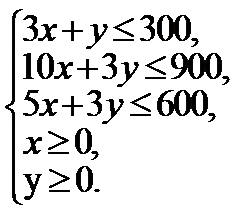
作出二元一次不等式组②表示的平面区域(如图),即可行域.
将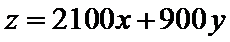
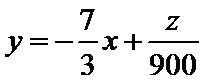
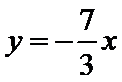
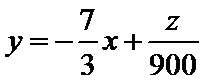
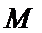
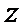
解方程组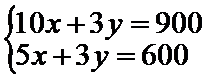
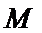
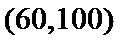
所以当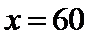
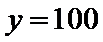
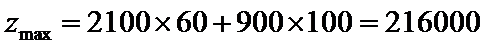
故生产产品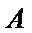
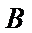
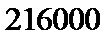
考查方向
解题思路
根据约束条件画出可行域,作出直线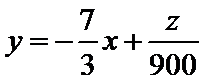
易错点
本题运算量较大,失分的一个主要原因是运算失误。
知识点
5.某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是()
(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg2≈0.30)
正确答案
解析
设第





考查方向
解题思路
本题考查等比数列的实际应用.在实际问题中平均增长率问题可以看作是等比数列的应用,解题时要注意把哪个作为数列的首项,然后根据等比数列的通项公式写出通项,列出不等式或方程就可解得结论.
易错点
本题考查等比数列的实际应用.在解指数型不等式时,不清楚两边同取对数的技巧。
知识点
9.设直线l1,l2分别是函数f(x)= 
正确答案
解析
由题设知:不妨设




得:





又



我们写出





此时点



①、②两式联立可解得交点


当且仅当

而

考查方向
解题思路
本题首先考查导数的几何意义,其次考查最值问题,解题时可设出切点坐标,利用切线垂直求出这两点的关系,同时得出切线方程,从而得点


易错点
本题首先考查导数的几何意义,容易在用导数后发生错误。
知识点
8.若
正确答案
解析
试题分析:用特殊值法,令






考查方向
解题思路
比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数函数单调性进行比较,若底数不同,可考虑利用中间量进行比较.
易错点
不能灵活应用函数的性质导致出错。
知识点
1.设

正确答案
解析



考查方向
解题思路
先去绝对值,然后利用不等式性质移项即可.
易错点
绝对值不等式的等价形式.
知识点
扫码查看完整答案与解析