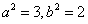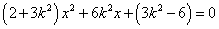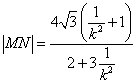- 一元二次不等式的解法
- 共209题
1
题型:简答题
|
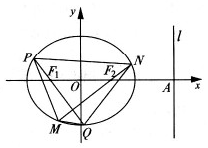
如图,F1、F2分别为椭圆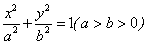
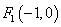
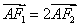
(1)求椭圆的方程;
(2)过F1、F2作互相垂直的两直线分别与椭圆交于P、Q、M、N四点,求四边形PMQN面积的取值范围。
正确答案
见解析。
解析
(1)由F1(-1,0)得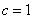
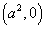
∵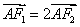
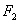
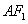
∴ 椭圆方程为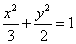
(2)当直线MN与PQ之一与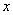
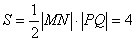
当直线PQ,MN均与
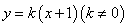
联立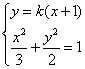
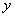
设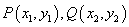
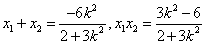
∴ 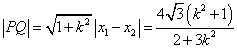
∴四边形PMQN面积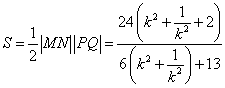
令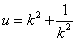
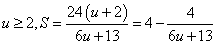
易知S是以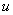
所以当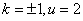
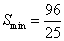
综上可知,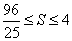

知识点
一元二次不等式的解法
1
题型:
单选题
|
设
正确答案
D
解析
略
知识点
一元二次不等式的解法
1
题型:填空题
|
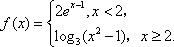
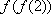
正确答案
2
解析
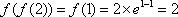
知识点
一元二次不等式的解法
1
题型:填空题
|
已知关于x的不等式|x+a|-|x-l|-a<2011 (a常数)的解集是R,则a的取值范围是
。
正确答案
解析
略
知识点
一元二次不等式的解法
1
题型:填空题
|
已知x,y满足不等式组
正确答案
9
解析
略
知识点
一元二次不等式的解法
已完结
扫码查看完整答案与解析