- 一元二次不等式的解法
- 共209题
已知数列


(e为自然对数的底





(1) 求证: 

(2)求证:

正确答案
见解析。
解析
(1) 


(2)由(1)得

综上所述,总有
解法二:
(2)

ii)假设

则n=k+1时要证明
只需证明:
即只需证明:


只需证明
只需证明
由
综合(i)(ii)可知

法三:
n=1时同法一:
当
只需证明
只需证明


由
综上所述

注1:

实际上
知识点
已知

正确答案
解析
解:∵f(﹣



又∵f(





∴则
故选C。
知识点
已知






正确答案
见解析
解析



由

由

∴当

当

知识点
已知数阵
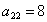
正确答案
解析
依题意得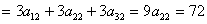
知识点
关于


(1)求实数
(2)若实系数一元二次方程


正确答案
见解析
解析
(1)原不等式等价于

由题意得,解集为

解得
(2)由题意得:

知识点
扫码查看完整答案与解析