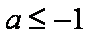一元二次不等式的解法
共209题

· 一元二次不等式的解法

一元二次不等式的解法
共209题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 13 分

设k∈R,函数 ,,x∈R.试讨论函数F(x)的单调性。

正确答案

见解析

解析

解析：，

对于，

当时，函数在上是增函数；

当时，函数在上是减函数，在上是增函数；

对于，

当时，函数在上是减函数；

当时，函数在上是减函数，在上是增函数。

知识点

一元二次不等式的解法

题型：简答题

简答题 · 10 分

已知直线的参数方程为为参数)，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，圆的极坐标方程为。

（1）求圆的直角坐标方程；

（2）若是直线与圆面≤的公共点，求的取值范围。

正确答案

（1）（2）

解析

（1）因为圆的极坐标方程为

所以

又

所以

所以圆的普通方程

（2）『解法1』：

设

由圆的方程

所以圆的圆心是，半径是

将代入得

又直线过，圆的半径是，所以

所以

即的取值范围是

『解法2』：

直线的参数方程化成普通方程为：…………6分

由，

解得，…………8分

∵是直线与圆面的公共点，

∴点在线段上，

∴的最大值是，

最小值是

∴的取值范围是…………10分

知识点

一元二次不等式的解法

题型：填空题

填空题 · 5 分

已知函数，则_______.

正确答案

解析

，

知识点

一元二次不等式的解法

题型：填空题

填空题 · 5 分

已知满足约束条件，且恒成立，则的取值范围为

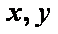
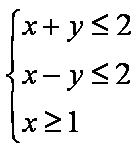
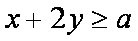
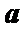
正确答案

解析

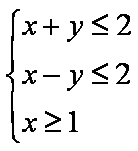
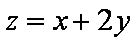
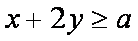
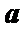
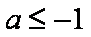
画出约束条件的可行域，由可行域知：过点（1，-1）时取最小值，且最小值为-1，所以要使恒成立，则的取值范围为。

知识点

一元二次不等式的解法

题型：简答题

简答题 · 13 分

某化工厂生产的某种化工产品，当年产量在150吨至此250吨之间，其生产的总成本y(万元)与年产量x（吨）之间的函数关系式可近似地表示为问：

（1）年产量为多少吨时，每吨的平均成本最低？并求出最低成本；

（2）每吨平均出厂价为16万元，年产量为多少（吨）时，可获得最大利润？并求出最大利润。

正确答案

见解析

解析

解析：（1）由题意可知，每吨平均成本为万元。

即≥-30=10

当且仅当，即x=200时，取“=”号，又因为200∈（150，250）所以年产量为200吨时，每吨的平均成本最低，最低成本为10万元。

（2）设年获得总利润为S万元，则S=

当∈（150，250）时，，故年产量为230吨时，可获得最大的利润为1290万元。

知识点

一元二次不等式的解法

题型：简答题

简答题 · 12 分

已知f(x)=m(x-2m)（x+m+3）,g(x)=-2，若同时满足条件：①x∈R，f(x) ＜0或g(x) ＜0；②x∈(﹣∝, ﹣4),f(x)g(x) ＜0。求m的取值范围。

正确答案

解析

解析：（1）由题意可知，时不能保证对＜0或＜0成立。

⑴当时，此时显然满足条件①；

⑵当－1＜＜0时，＞要使其满足条件①，则需－1＜＜0且＜1，解得－1＜＜0；

⑶当＜－1时，＞，要使其满足条件①，则需＜－1且＜1，

解得－4＜＜－1.　因此满足条件①的的取值范围为

（2）在满足条件①的前提下，再探讨满足条件②的取值范围。

⑴当时，在上，与均小于0，不合题意；

⑵当＜－1时，则需＜－4，即＜－2，所以－4＜＜－2.

⑶当－1＜＜0时，则需＜－4，即＞1，此时无解。

综上所述满足①②两个条件的的取值范围为

知识点

一元二次不等式的解法

题型：单选题

单选题 · 5 分

函数的图象可能是

正确答案

解析

略

知识点

一元二次不等式的解法

题型：填空题

填空题 · 5 分

已知实数满足，则目标函数的最大值为

正确答案

解析

确定可行域为点形成的三角形，则过时取到最大值为

知识点

一元二次不等式的解法

题型：单选题

单选题 · 5 分

已知集合A={x|+x-2＜0}，集合B={x|}，则(CRA)∩B=

A{x|2≤x＜3}

B{x|1≤x＜3}

C{x|-2＜x＜1}

D{x|-2＜x≤-1或2≤x＜3}

正确答案

解析

∵A＝{x|－2＜x＜1}，B＝{x|－2＜x＜3}，∴(RA)∩B＝{x|1≤x＜3}。

知识点

一元二次不等式的解法

题型：简答题

简答题 · 10 分

已知，，，且。

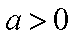
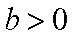
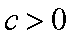
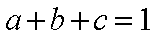
（1）求证：；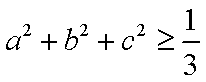

（2）求证：。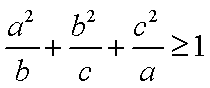

正确答案

见解析

解析

证明：（1）∵，，，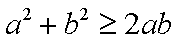

∴，

∵，∴，

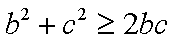
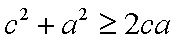
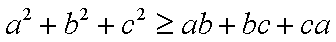
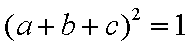
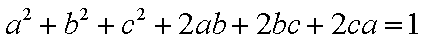
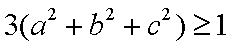
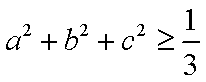
∴，即；

（2）∵，，，

∴，即，

∵，∴。

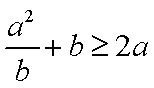
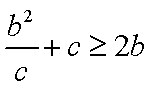
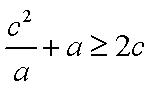
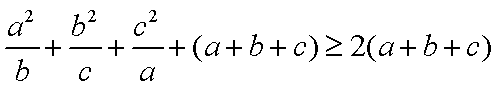
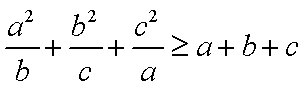
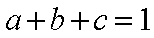
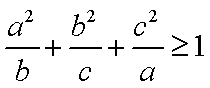
知识点

一元二次不等式的解法

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 一元二次不等式的解法

扫码查看完整答案与解析