一元二次不等式的解法
共209题

· 一元二次不等式的解法

一元二次不等式的解法
共209题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 10 分

已知直线的参数方程为为参数)，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，圆的极坐标方程为。

（1）求圆的直角坐标方程；

（2）若是直线与圆面≤的公共点，求的取值范围。

正确答案

（1）（2）

解析

（1）因为圆的极坐标方程为

所以

又

所以

所以圆的普通方程

（2）『解法1』：

设

由圆的方程

所以圆的圆心是，半径是

将代入得

又直线过，圆的半径是，所以

所以

即的取值范围是

『解法2』：

直线的参数方程化成普通方程为：…………6分

由，

解得，…………8分

∵是直线与圆面的公共点，

∴点在线段上，

∴的最大值是，

最小值是

∴的取值范围是…………10分

知识点

一元二次不等式的解法

题型：填空题

填空题 · 5 分

已知函数，则_______.

正确答案

解析

，

知识点

一元二次不等式的解法

题型：填空题

填空题 · 5 分

已知满足约束条件，且恒成立，则的取值范围为

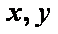
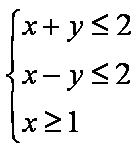
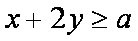
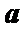
正确答案

解析

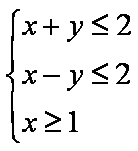
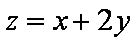
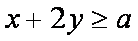
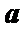
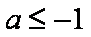
画出约束条件的可行域，由可行域知：过点（1，-1）时取最小值，且最小值为-1，所以要使恒成立，则的取值范围为。

知识点

一元二次不等式的解法

题型：填空题

填空题 · 5 分

已知实数满足，则目标函数的最大值为

正确答案

解析

确定可行域为点形成的三角形，则过时取到最大值为

知识点

一元二次不等式的解法

题型：简答题

简答题 · 10 分

已知，，，且。

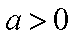
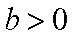
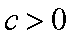
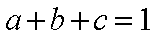
（1）求证：；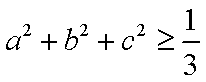

（2）求证：。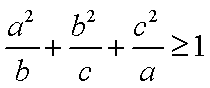

正确答案

见解析

解析

证明：（1）∵，，，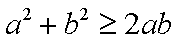

∴，

∵，∴，

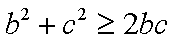
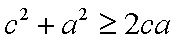
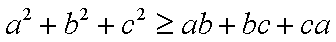
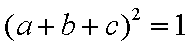
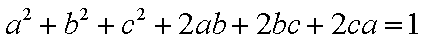
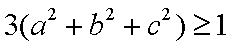
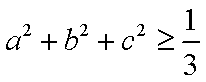
∴，即；

（2）∵，，，

∴，即，

∵，∴。

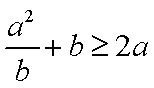
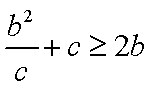
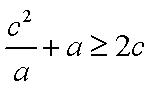
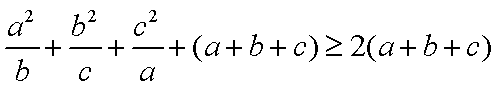
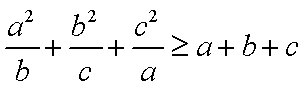
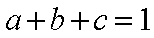
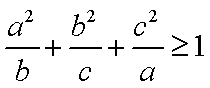
知识点

一元二次不等式的解法

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 一元二次不等式的解法

扫码查看完整答案与解析