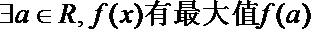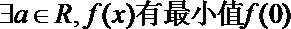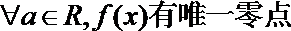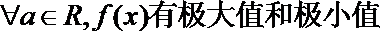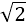- 函数的最值
- 共119题
17．已知幂函数
（1）求函数
（2）设函数
正确答案
（1）幂函数
且在区间
又
(2）
由题，
解析
解析已在路上飞奔，马上就到！
知识点
9．已知函数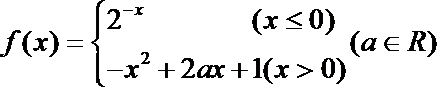
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17. 已知
（1）求数量积
（2）求
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21．如图，已知抛物线
（Ⅰ）求⊙M和抛物线
（Ⅱ）若
（Ⅲ）过
正确答案
解：（Ⅰ）因为
设⊙M的半径为
（Ⅱ）设
所以当
（Ⅲ）以点Q这圆心,QS为半径作⊙Q,则线段ST即为⊙Q与⊙M的公共弦
设点
从而直线QS的方程为
因为
解析
解析已在路上飞奔，马上就到！
知识点
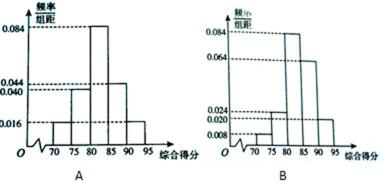
18．了响应政府“节能、降耗、减排、增效”的号召，某工厂决定转产节能灯，现有A，B两种型号节能灯的生产线供选择；从这两种生产线生产的大量节能灯中各随机抽取100个进行质量评估，经检验，综合得分情况如下面的频率分布直方图：
产品级别划分以及利润如下表：
视频率为概率．
（1）估计生产A型节能灯的一级品率．
（2）估计生产一个B型节能灯的利润大于0的概率，并估计生产品100个B型节能灯的平均利润。
正确答案
解：
解析
解析已在路上飞奔，马上就到！
知识点
10．在
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10.若函数f(x)=x2-ax+2在区间[0，1]上至少有一个零点，则实数a的取值范围是___________.
正确答案
[3,+∞)
解析
由题意,知关于x的方程x2-ax+2=0在区间[0,1]上有实数解.
又x=0不是方程x2-ax+2=0的解,
所以根据0<x≤1可将方程x2-ax+2=0变形为a=
从而问题转化为求函数g(x)=x+
因为函数g(x)在(0,1]上单调递减,所以g(x)∈[3,+∞).
故所求实数a的取值范围是[3,+∞).
知识点
11.记min{a，b}为a、b两数的最小值，当正数x、y变化时，t=min{x，
A
B
C
D
正确答案
解析
（1）若x≤
（2）若
综上可知，当x=y=
知识点
4.若直线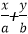
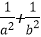
A
B1
C
D
正确答案
解析
设向量m=(cosα，sinα)，n=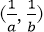
由题意知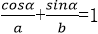
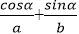
即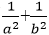
知识点
11.记min{a，b}为a、b两数的最小值，当正数x、y变化时，t=min{x，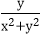
A
B
C
D
正确答案
解析
（1）若x≤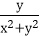
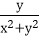
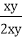
故t≤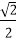
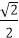
（2）若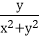
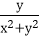
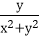
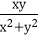
故t≤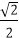
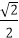
综上可知，当x=y=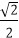
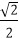
知识点
扫码查看完整答案与解析