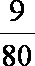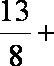- 函数的最值
- 共119题
设






















正确答案
解析
由题设知结论①显然成立,对于②,先求b、c中的最大者再与














知识点
已知函数
(1)当a=1时,求
(2)若在区间


正确答案
见解析。
解析
(1)当



所以



(2)令

在区间




∵
① 若

当


此时


当




②若





要使

此时求得

综合①②可知,当


知识点
设函数
(1)若函数y=f(x)在x=﹣1处取得极值,求a的值;
(2)已知函数f(x)有3个不同的零点,分别为0、x1、x2,且x1<x2,若对任意的x∈[x1,x2],f(x)>f(1)恒成立,求a的取值范围。
正确答案
见解析。
解析
(1)求导函数,可得f′(x)=﹣x2+2x+(a2﹣1)
∵函数y=f(x)在x=﹣1处取得极值,
∴f′(﹣1)=0
∴﹣1﹣2+(a2﹣1)=0
∴a=±2
经检验,a=2符合题意;
(2)由题意,

∵函数f(x)有3个不同的零点,分别为0、x1、x2,
∴
∴△=1+

且x1+x2=3
∵x1<x2,∴2x2>x1+x2=3,∴x2>
①若x1≤1<x2,则f(1)=
②若1<x1<x2,则对任意的x∈[x1,x2],有x﹣x1≥0,x﹣x2≤0,
∴
又f(x1)=0,∴f(x)在[x1,x2]上的最小值为0
∴对任意的x∈[x1,x2],f(x)>f(1)恒成立,等价于f(1)=
∴
综上可得a的取值范围为
知识点
若
(1)讨论
(2)当



正确答案
见解析。
解析
由
(1))令
则
①当


故
所以
所以

②当


故
所以
所以

③当

又因为

(i)当

当

所以

(ii) 当
令
令
故此时
减区间为
综上得:①当


②当

减区间为
③当


(2)因为在
所以
即
整理得
当
所以
知识点
在约束条件
正确答案
解析
由约束条件得如图所示的三角形区域,
令2x+y=z,y=﹣2x+z,
显然当平行直线过点B(
z取得最大值为2;
当平行直线过点B(0,
z取得最小,但B点不在可行域内;
故选A
知识点
已知函数
(1)若曲线


(2)在(1)的条件下,试求函数
(m为实常数,
(3)若


正确答案
见解析。
解析
(1)











由①②得:
(2)由(1)知:




当





由表可知:

当




由表可知:
综上可知:当


当
(3)因为


即

∴
由 (1)+(3)得:
由(4)得:



故
知识点
已知函数
(1)求函数
(2)设











正确答案
(1)-2,
解析
解析:(1)
则

(2)








由余弦定理,得

由①②解得
知识点
如图,已知

(1)求异面直线

(2)求三棱锥

正确答案
(1)
解析


连接
则

由题意得


所以,异面直线

(2)由题意得,




三棱锥

知识点
数列



(1)当


(2)若数列

(3)当

正确答案
见解析
解析
(1)


(2)当

(3)





当

知识点
设函数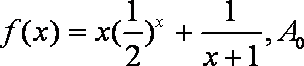
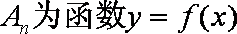
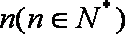
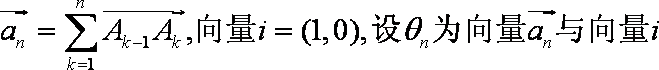

正确答案
3
解析
由题意知An=(n,f(n)),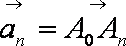
tanθn=
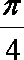
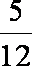
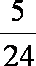
则有 1+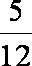
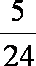
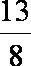

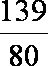
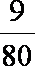
知识点
扫码查看完整答案与解析