- 函数的最值
- 共119题
已知函数
(1)求函数

(2)求
(3)设实数


正确答案
见解析。
解析
(1)



(2)令



当


(3)∵a>0,由(2)知:F(x)在(0,e)上单调递增,在(e,+∞)上单调递减,



当2<a时,
(3)另法:①2 a<e,即
②

1° 



③





知识点
设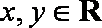
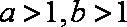
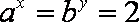
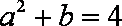
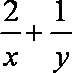
正确答案
解析
由题意得: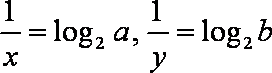
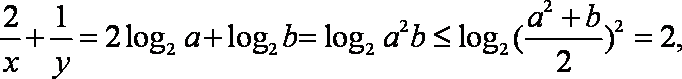
知识点
已知


(1) 求

(2)设函数




正确答案
(1)
解析
解析:(1)



∴



当

所以函数



(2)由(1)知:函数

∴ 
又 函数
① 当


②当





(3)当




∴

所以,

知识点
已知椭圆G:


(1)求椭圆G的方程;
(2)在直线l的斜率k变化的过程中,是
个常数

这个常数
正确答案
见解析
解析
(1)解:设





(2)存在常数
解法一:设

于是 
直线AM的斜率

则


同理可得

同理可得

综上可知,存在常数
解法二:设

于是 
A、B关于x轴的对称点分别为



所以







知识点
设递增等差数列






(1)求数列
(2)求数列


正确答案
见解析。
解析
在递增等差数列

解得 



知识点
已知函数
(1)若x<a时,f(x)<1恒成立,求实数a的取值范围;
(2)若a≥﹣4时,函数f(x)在实数集R上有最小值,求实数a的取值范围
正确答案
见解析。
解析
(1)因为x<a时,f(x)=4x﹣4×2x﹣a,所以令2x=t,则有0<t<2a,
所以f(x)<1当x<a时恒成立,可转化为
即
令

所以
所以

所以

所以
(2)当x≥a时,f(x)=x2﹣ax+1,即
①当
所以f(x)min=f(a)=1;
②当



所以由①②可得:当x≥a时有:
当x<a时,f(x)=4x﹣4×2x﹣a,令2x=t,t∈(0,2a),则
③当




④当

所以,此时,h(t)在(0,2a)上无最小值;
所以由③④可得当x<a时有:当

当
所以,由①②③④可得:
当


当
当﹣4≤a<0时,
综上所述,当


所以函数f(x)在实数集R上有最小值时,实数a的取值范围为
知识点
要得到函数

正确答案
解析
将


知识点
下列命题:① 若函数













正确答案
解析
函数





知识点
设x,y满足约束条件
正确答案
26
解析
作出不等式组
得到如图的△ABC及其内部,
其中A(2,0),B(4,6),C(0,2),O为坐标原点
设z=F(x,y)=2x+3y,将直线l:z=2x+3y进行平移,
当l经过点B时,目标函数z达到最大值
∴z最大值=F(4,6)=26
故答案为:26
知识点
已知
(1)当

(2) 求函数

(3) 证明: 对一切

正确答案
见解析。
解析
(1)∵

当


故

(2)






① 
② 


③ 




知识点
扫码查看完整答案与解析




























