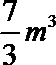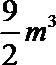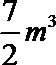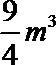- 组合几何体的面积、体积问题
- 共98题
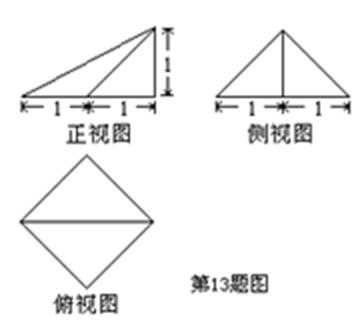
13．一个几何体的三视图如图所示，则该几何体的体积为____．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
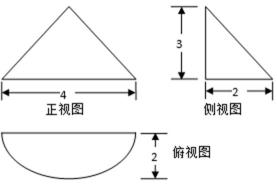
13．若某几何体的三视图 (单位：cm) 如图所示，则此几何体的表面积是__________cm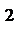
正确答案
2π
解析
解析已在路上飞奔，马上就到！
知识点
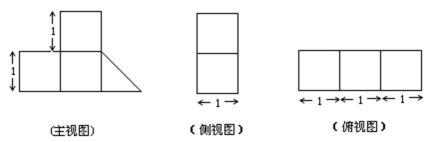
14．已知几何体的三视图如图所示，可得这个几何体的体积是 ___________
正确答案
6
解析
解析已在路上飞奔，马上就到！
知识点
4．已知某几何体的三视图如图所示，则其体积为 （ ）
A8
B4
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．下图是底面半径为1，母线长均为2的圆锥和圆柱的组合体，则该组合体的体积为__________。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．如图，AD
（1）求证：AF∥平面BDE；
（2）求证：平面BDE
正确答案
（1）证明：∵AD⊥平面ABC，AC
∴AD⊥AC，AD⊥AB，
∵AD∥CE，∴CE⊥AC
∴四边形ACED为直角梯形.
又∵∠BAC=90°，∴AB⊥AC，∴AB⊥面ACED.
∴凸多面体ABCED的体积
求得CE=2.
取BE的中点G，连结GF，GD，
则GF∥EC，GF
∴GF∥AD，GF=AD，四边形ADGF为平行四边形，
∴AF∥DG.
又∵GD
∴AF∥平面BDE.
（2）证明：∵AB=AC，F为BC的中点，
∴AF⊥BC.
由（1）知AD⊥平面ABC，AD∥GF，∴GF⊥面ABC.
∵AF
又BC
又∵DG∥AF，∴DG⊥面BCE.
∵DG
解析
解析已在路上飞奔，马上就到！
知识点
4．一个几何体按比例绘制的三视图如图所示（单位：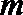
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x的值是（ ）
A2
B
C
D3
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．某几何体的三视图如图所示，则该几何体的表面积为（ ）
A
B2
C（2
D（2
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4.已知某几何体的三视图如图所示，则该几何体的体积为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析