- 组合几何体的面积、体积问题
- 共98题
1
题型:填空题
|
13.若某几何体的三视图 (单位:cm) 如图所示,则此几何体的表面积是__________cm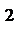
正确答案
2π
解析
解析已在路上飞奔,马上就到!
知识点
组合几何体的面积、体积问题简单空间图形的三视图
1
题型:填空题
|
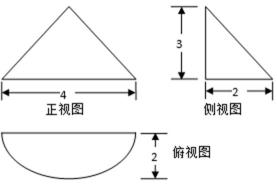
14.已知几何体的三视图如图所示,可得这个几何体的体积是 ___________
正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
组合几何体的面积、体积问题简单空间图形的三视图
1
题型:
单选题
|
4.已知某几何体的三视图如图所示,则其体积为 ( )
正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
组合几何体的面积、体积问题简单空间图形的三视图
1
题型:填空题
|
7.下图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的体积为__________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
组合几何体的面积、体积问题
1
题型:简答题
|
18.如图,AD

(1)求证:AF∥平面BDE;
(2)求证:平面BDE
正确答案
(1)证明:∵AD⊥平面ABC,AC

∴AD⊥AC,AD⊥AB,
∵AD∥CE,∴CE⊥AC
∴四边形ACED为直角梯形.
又∵∠BAC=90°,∴AB⊥AC,∴AB⊥面ACED.
∴凸多面体ABCED的体积
求得CE=2.
取BE的中点G,连结GF,GD,
则GF∥EC,GF
∴GF∥AD,GF=AD,四边形ADGF为平行四边形,
∴AF∥DG.
又∵GD

∴AF∥平面BDE.
(2)证明:∵AB=AC,F为BC的中点,
∴AF⊥BC.
由(1)知AD⊥平面ABC,AD∥GF,∴GF⊥面ABC.
∵AF
又BC
又∵DG∥AF,∴DG⊥面BCE.
∵DG
解析
解析已在路上飞奔,马上就到!
知识点
组合几何体的面积、体积问题直线与平面平行的判定与性质直线与平面垂直的判定与性质平面与平面垂直的判定与性质
下一知识点 : 构成空间几何体的基本元素
扫码查看完整答案与解析