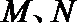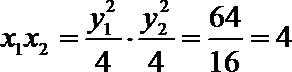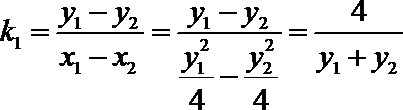直线与圆锥曲线的位置关系
共218题

直线与圆锥曲线的位置关系
共218题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

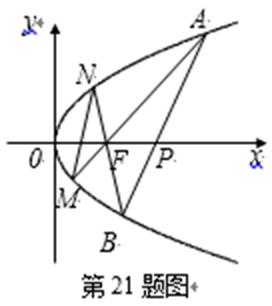
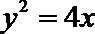
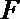
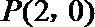
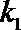
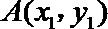
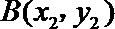
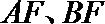
21．如图，已知抛物线的焦点为，过点且斜率为的直线交抛物线于，两点，直线分别与抛物线交于点

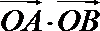
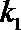
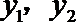
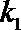
（1）证明的值与无关，并用表示；

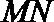
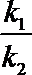
（2）记直线的斜率为，证明为定值．

正确答案

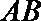
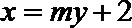
证明：（1）依题意，设直线的方程为．

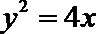
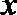
将其代入，消去，整理得．

从而．于是

∴与无关，

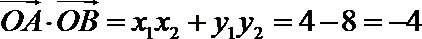
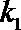
又

（2）证明：设，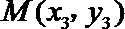

则．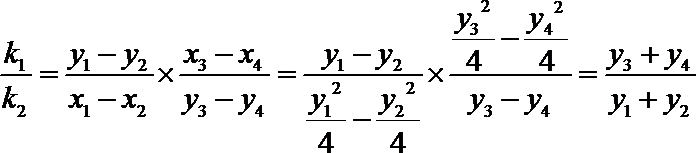

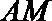
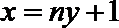
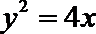
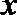
设直线的方程为，将其代入，消去，

整理得

∴．同理可得．

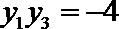
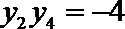
故．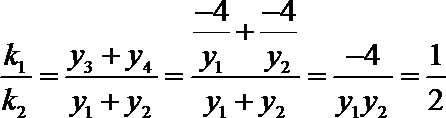

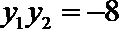
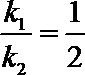
由（1）知，，∴为定值．

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率抛物线焦点弦的性质直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题

题型：填空题

填空题 · 4 分

15．过椭圆的右焦点作一条斜率为2的直线与椭圆交于两点，为坐标原点，则的面积为( )。

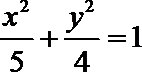
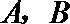
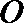
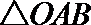
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的几何性质直线与圆锥曲线的综合问题

题型：简答题

简答题 · 12 分

21．已知圆:交轴于A,B两点,曲线是以AB为长轴,离心率为的椭圆,其左焦点为F,若P是圆上一点,连结PF,过原点作直线PF的垂线交直线x=-2于点Q.

（Ⅰ）求椭圆的标准方程；

（Ⅱ）当点P在圆上运动时（不与A、B重合）,求证:直线PQ与圆相切。

正确答案

解:（Ⅰ）因为,所以c=1,则b=1,

所以椭圆C的标准方程为

（Ⅱ）当点P在圆O上运动时,

设（）,则,

所以,,

所以直线OQ的方程为所以点Q（-2,）

所以,又

所以,即OP⊥PQ,

当，，故直线PQ始终与圆O相切

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题直线、圆及圆锥曲线的交汇问题

题型：简答题

简答题 · 12 分

20．已知椭圆的左、右顶点分别为曲线是以椭圆中心为顶点，为焦点的抛物线．

（Ⅰ）求曲线的方程；

（Ⅱ）若直线与曲线交于不同的两点且，求实数的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算椭圆的几何性质抛物线的标准方程和几何性质直线与圆锥曲线的综合问题圆锥曲线中的范围、最值问题

题型：简答题

简答题 · 12 分

19．设椭圆焦点坐标为F1（-c,0）, F2（c,0）,点Q是椭圆短轴上的顶点，且满足．

（1）求椭圆的方程；

（2）设A,B是圆与与y轴的交点，是椭圆上的任一点，求的最大值。

正确答案

（1），

故a2=8+8=16,故椭圆方程为：．

（2）令x=0,得y=3或y=1．故A（0，3）,B（0，1）．

设P（x,y）,则=（-x,3-y）·(-x,1-y)=x2+(3-y)(1-y)= x2+y2-4y+3．

又，故x2=16-2 y2．

所以=16-2 y2+y2-4y+3=-2（y+1）2+21

又，故y=-1时，取最大值21．

解析

解析已在路上飞奔，马上就到！

知识点

向量在几何中的应用椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线中的范围、最值问题直线、圆及圆锥曲线的交汇问题

题型：简答题

简答题 · 13 分

20．已知椭圆C：的一个焦点是（1，0），两个焦点与短轴的一个端点构成等边三角形．

（1）求椭圆C的方程；

（2）过点Q（4，0）且不与坐标轴垂直的直线l交椭圆C于A、B两点，设点A关于x轴的对称点为。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程椭圆的几何性质直线与圆锥曲线的综合问题圆锥曲线中的范围、最值问题圆锥曲线的定点、定值问题

题型：填空题

填空题 · 5 分

13．过抛物线的焦点的直线交抛物线于两点，若抛物线在点处的切线斜率为1，则线段。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的标准方程和几何性质直线与圆锥曲线的综合问题

题型：单选题

单选题 · 5 分

4.对抛物线，下列描述正确的是（）

A开口向上，焦点为

B开口向上，焦点为

C开口向右，焦点为

D开口向右，焦点为

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与圆锥曲线的综合问题

题型：填空题

填空题 · 5 分

15.设是焦距等于6的双曲线的两个焦点，是上一点，若，且的最小内角为，则的方程为_________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程直线与圆锥曲线的综合问题

题型：简答题

简答题 · 14 分

21．已知抛物线的焦点以及椭圆的上、下焦点及左、右顶点均在圆上．

（1）求抛物线和椭圆的标准方程；

（2）过点的直线交抛物线于两不同点，交轴于点，已知，，求的值；

（3）直线交椭圆于、两个不同点，、在轴的射影分别为、，且，若点满足，证明：点在椭圆上。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算向量在几何中的应用椭圆的定义及标准方程抛物线的标准方程和几何性质直线与圆锥曲线的综合问题

继续学习学习下一知识点

下一知识点 : 曲线与方程

百度题库 > 高考 > 文科数学 > 直线与圆锥曲线的位置关系

扫码查看完整答案与解析