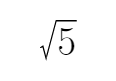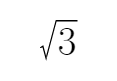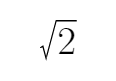直线与圆锥曲线的位置关系
共218题

直线与圆锥曲线的位置关系
共218题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

10. 双曲线的左、右焦点分别为F1，F2,渐近线分别为，点P在第一象限内且在上，若⊥PF1，∥PF2，则该双曲线的离心率为（）

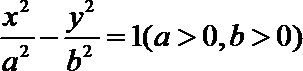
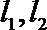
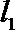
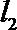
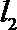
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的几何性质直线与圆锥曲线的综合问题

题型：简答题

简答题 · 12 分

18．如图，直线l ：y=x+b与抛物线C ：x2=4y相切于点A。

（1）求实数b的值；

（2）求以点A为圆心，且与抛物线C的准线相切的圆的方程。

正确答案

（1）由得（）

因为直线与抛物线C相切

所以

解得

（2）由（1）可知

故方程（）即为

解得，将其代入

得y=1

故点A（2，1）

因为圆A与抛物线C的准线相切

所以圆心A到抛物线C的准线y=-1的距离等于圆A的半径r

即r=|1-（-1）|=2

所以圆A的方程为

解析

解析已在路上飞奔，马上就到！

知识点

圆的标准方程抛物线的标准方程和几何性质直线与圆锥曲线的综合问题直线、圆及圆锥曲线的交汇问题

题型：简答题

简答题 · 13 分

21．设，是椭圆上的两点，，，且，椭圆离心率，短轴长为2，O为坐标原点．

（Ⅰ）求椭圆方程；

（Ⅱ）若直线AB过椭圆的焦点（为半焦距），求直线AB的斜率；

（Ⅲ）试问的面积是否为定值？若是，求出该定值；若不是，请说明理由．

正确答案

解：（Ⅰ）由，解得，∴所求椭圆的方程为

（Ⅱ）设AB的方程为，则

，．

由已知：

解得

（Ⅲ）当A为顶点时，B必为顶点，则，

当A．B不为顶点时，设AB方程为y=kx+m，

由

，．

又，即，知

∴三角形的面积为定值1

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题

题型：简答题

简答题 · 13 分

21．已知点和直线，作垂足为Q，且

（Ⅰ）求点P的轨迹方程；

（Ⅱ）过点C的直线m与点P的轨迹交于两点点，若的面积为，求直线的方程．

正确答案

解：（Ⅰ）由已知知．

所以，设，代入上式得

平方整理得．

（Ⅱ）由题意可知设直线的斜率不为零，且恰为双曲线的右焦点，

设直线的方程为，

由

若，则直线与双曲线只有一个交点，这与矛盾，故．

由韦达定理可得

故直线的方程为．

解析

解析已在路上飞奔，马上就到！

知识点

直线的一般式方程双曲线的定义及标准方程直线与圆锥曲线的综合问题直接法求轨迹方程

题型：简答题

简答题 · 13 分

20．已知椭圆的两个焦点分别为，点P在椭圆上，且满足，直线与圆相切，与椭圆相交于两点．

（I）求椭圆的方程；

（II）证明为定值（为坐标原点）．

正确答案

解：（I）由题意，，

解三角形得，由椭圆定义得，

从而又，则，所以椭圆的方程为

（II）设交点，

联立消去得

由韦达定理得

又直线与圆相切，

则有

从而

所以，即为定值．

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题直线、圆及圆锥曲线的交汇问题

题型：单选题

单选题 · 5 分

10．已知双曲线的右焦点为F,若过点F且倾斜角为的直线与双曲线右支有且仅有一个交点,则此双曲线的离心率的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的几何性质直线与圆锥曲线的综合问题

题型：简答题

简答题 · 15 分

19. 已知椭圆E：的左焦点为F，左准线l与x轴的交点是圆C的圆心，圆C恰好经过坐标原点O，设G是圆C上任意一点。

（1）求圆C的方程；

（2）若直线FG与直线l交于点T，且G为线段FT的中点，求直线FG被圆C所截得的弦长；

（3）在平面上是否存在定点P，使得？若存在，求出点P坐标；若不存在，请说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

圆的标准方程直线与圆相交的性质椭圆的几何性质直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题

题型：填空题

填空题 · 5 分

8.已知椭圆C: 的左,右焦点分别为F1,F2,动直线l:y=x+m与椭圆C相切,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l.则四边形F1MNF2的面积为________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的几何性质直线与椭圆的位置关系直线与圆锥曲线的综合问题

题型：单选题

单选题 · 5 分

4.过双曲线x2－=1的右焦点F作直线l交双曲线于A，B两点，若2<|AB|<4，则这样的直线l共有（）

A1条

B2条

C3条

D4条

正确答案

解析

当|AB|=2时，只有一条，此时是x轴；

当|AB|=4时，有三条，其中两条交在两支上，另一条垂直于x轴.

那么当2<|AB|<4时，有两条.

知识点

双曲线的几何性质直线与圆锥曲线的综合问题

题型：单选题

单选题 · 5 分

2.y=kx+2与交于A、B两点，且kOA+kOB=3，则直线AB的方程为（）

A2x-3y-4=0

B2x+3y-4=0

C3x+2y-4=0

D3x-2y-4=0

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的几何性质直线与圆锥曲线的综合问题

继续学习学习下一知识点

下一知识点 : 曲线与方程

百度题库 > 高考 > 文科数学 > 直线与圆锥曲线的位置关系

扫码查看完整答案与解析