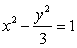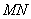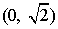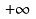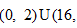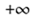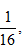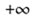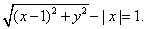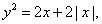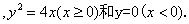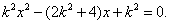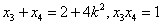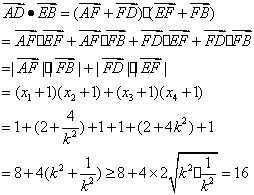- 直线与圆锥曲线的位置关系
- 共218题
10.已知点






正确答案
解析
由







考查方向
解题思路
1.先根据题中给出的条件求出
易错点
1.不会利用椭圆的定义这一隐含条件解决问题;
2.不能从题中给出的条件
知识点
21.曲线C:x|x|+y|y|=1
(I) 直线x+y-b=0与曲线C交于A,B两点用b表示|AB|的长;
(II) 分别过A,B作直线x+y=0的垂线,垂足分别为C,D,求四边形ABCD面积的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
在图(1)的程序框图中,任意输入一次

则能输出数对
正确答案
解析
结合图易得所求概率为
知识点
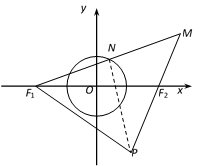
(1)已知定点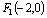
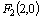
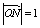
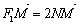
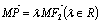
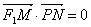
(2)如图,已知椭圆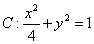
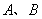
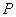
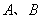
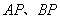
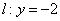
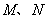
(ⅰ)设直线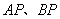
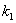
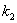
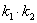
(ⅱ)当点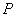

正确答案
见解析。
解析
(1)连接ON∵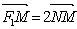
∵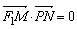
∴|∣PF1|-|PF2∣|=||PM|-|PF2||=|MF2|=2<|F1F2
由双曲线的定义可知:点P的轨迹是以F1,F2为焦点的双曲线。
点P的轨迹方程是
(2)(ⅰ)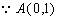
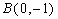
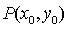
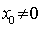
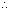
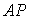
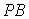
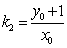
又点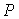
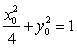
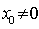
从而有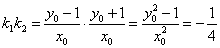
(ⅱ)设点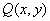
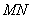
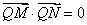
得
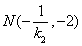
所以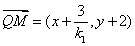
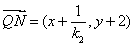
故有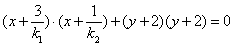
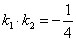
为直径的圆的方程为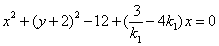
令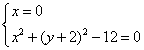
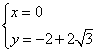
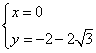
所以以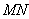
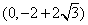
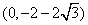
知识点
设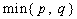
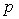
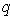
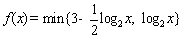
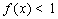
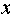
正确答案
解析
略
知识点
8. 过双曲线
正确答案
解析
双曲线的两个顶点之间的距离为2,小于4,所以过抛物线的焦点一定有两条直线使得交点之间的距离等于4,当直线与实轴垂直式,可以知道直线AB的长度是4,综上可知,有三条直线满足AB=4
考查方向
解题思路
考虑全面,确定边界情况。
易错点
考虑情况不全面
知识点
阅读右图所示的程序框图,运行相应的程序,输出的结果是
正确答案
解析
知识点
某程序框图如图所示,该程序运行后输出k的值是
正确答案
解析
略
知识点
设a,b是关于t的方程t2cosθ+tsinθ=0的两个不等实根,则过A(a,a2),B(b,b2)两点的直线与双曲线

正确答案
解析
∵a,b是关于t的方程t2cosθ+tsinθ=0的两个不等实根,
∴a+b=﹣
过A(a,a2),B(b,b2)两点的直线为y﹣a2=
即y=﹣
∵双曲线


∴过A(a,a2),B(b,b2)两点的直线与双曲线

知识点
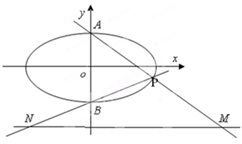
已知平面内一动点
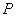
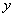
(1)求动点
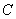
(2)过点

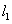
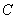

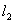
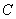
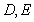
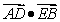
正确答案
(1) 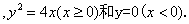
解析
(1)设动点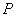
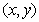
化简得
当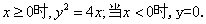
所以动点P的轨迹C的方程为
(2)由题意知,直线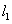
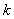
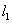
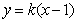
由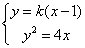
设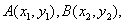
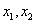
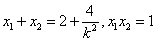
因为
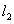
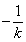
设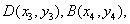
故
当且仅当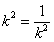
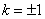
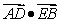
知识点
扫码查看完整答案与解析