- 直线与圆锥曲线的位置关系
- 共218题
4.若一个圆锥的侧面积是底面积的3倍,则圆锥的母线与轴的夹角的大小为__________ (用反三角形式表示)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
若圆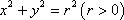
正确答案
解析
略。
知识点
设抛物线












(1)若




(2)若









正确答案
(1)
解析
设准线


则|FE|=


(1) ∵



设A(


∵






∴F(0,1), FA|=

(2) 解析1∵






由抛物线定义知




∴直线




设直线



∵




∴直线




∴坐标原点到

解析2由对称性设
点

得:

直线
坐标原点到

知识点
直线

正确答案
解析
画出不等式组
因为直线



知识点
设向量




正确答案
解析

知识点
设


正确答案
解析
略
知识点
已知三点O(0,0),A(-2,1),B(2,1),曲线C上任意一点M(x,y)满足
(1)求曲线C的方程;
(2)点Q(x0,y0)(-2<x0<2)是曲线C上的动点,曲线C在点Q处的切线为l,点P的坐标是(0,-1),l与PA,PB分别交于点D,E,求△QAB与△PDE的面积之比。
正确答案
(1) x2=4y; (2)2
解析
(1)由

得

由已知得
化简得曲线C的方程:x2=4y.
(2)直线PA,PB的方程分别是y=-x-1,y=x-1,曲线C在Q处的切线l的方程是

分别联立方程组


则xE-xD=2,|FP|=1-
故S△PDE=


则
知识点
已知圆锥母线长为6,底面圆半径长为4,点





(1)求圆的侧面积和体积。
(2)求异面直线

正确答案
(1)

解析
(1)圆锥的侧面积

(2) 连





又,








当


当


综上异面直线



知识点
某商场为吸引顾客消费推出一项优惠活动,活动规则如下:消费每满100元可以转动如图所示的圆盘一次,其中O为圆心,且标有20元、10元、0元的三部分区域面积
相等, 假定指针停在任一位置都是等可能的,当指针停在某区域时,返相应金额的优惠券,(例如:某顾客消费了218元 ,第一次转动获得了20元,第二次获得了10元,
则其共获得了30元优惠券,)顾客甲和乙都到商场进行了消费,并按照规则参与了活动。
正确答案
见解析。
解析
(1)设“甲获得优惠券”为事件A.
因为假定指针停在任一位置都是等可能的,而题中所给的三部分的面积相等,
所以指针停在20元,10元,0元区域内的概率都是
顾客甲获得优惠券,是指指针停在20元或10元区域,
根据互斥事件的概率,有
所以顾客甲获得优惠券面额大于0元的概率是
(2)设“乙获得优惠券金额不低于20元”为事件B
因为顾客乙转动了转盘两次,设乙第一次转动转盘获得优惠券金额为
第二次获得优惠券金额为

即

而乙获得优惠券金额不低于20元,是指
所以事件B中包含的基本事件有6个,
所以乙获得优惠券额不低于20元的概率为
故甲获得优惠券面额大于0元的概率为

知识点
已知抛物线



(1)求

(2)如图,设直线








正确答案
见解析。
解析
(1)焦点





(2)联立











知识点
扫码查看完整答案与解析





































